Baumdiagramm

Bei mehrstufigen Zufallsexperimenten können zur Visualisierung Baumdiagramme verwendet werden. Baumdiagramme beginnen an einem Startpunkt von dem Äste abgehen. Auf einem Ast steht die Wahrscheinlichkeit, dass das Ereignis zu welchem dieser führt eintritt. Am Ende eines Astes können neue Äste beginnen. Bei diesen neuen Ästen wird für die Wahrscheinlichkeit angenommen, dass man schon am Knotenpunkt angekommen ist. Die Wahrscheinlichkeit der Äste, die von einem Knotenpunkt ausgehen, ergibt summiert 1 (bei zwei Ästen sind die beiden Ereignisse zu denen sie führen so Gegenereignisse zueinander). Auf diesen Ästen findet sich die bedingte Wahrscheinlichkeit $(P_{B}(A)$)). Am Ende des Astes befindet sich ein Ereignis, dessen Wahrscheinlichkeit durch die erste Pfadregel berechnet werden kann, sie ist also das Produkt aller Werte der vorherigen Pfade, die Schnittmenge aller Ereignisse auf diesem Pfad. Die Wahrscheinlichkeit für ein mehrere Versuchsausgänge erfassendes Ereignis wird durch Addition der Wahrscheinlichkeiten der einzelnen Versuchsausgänge addiert.

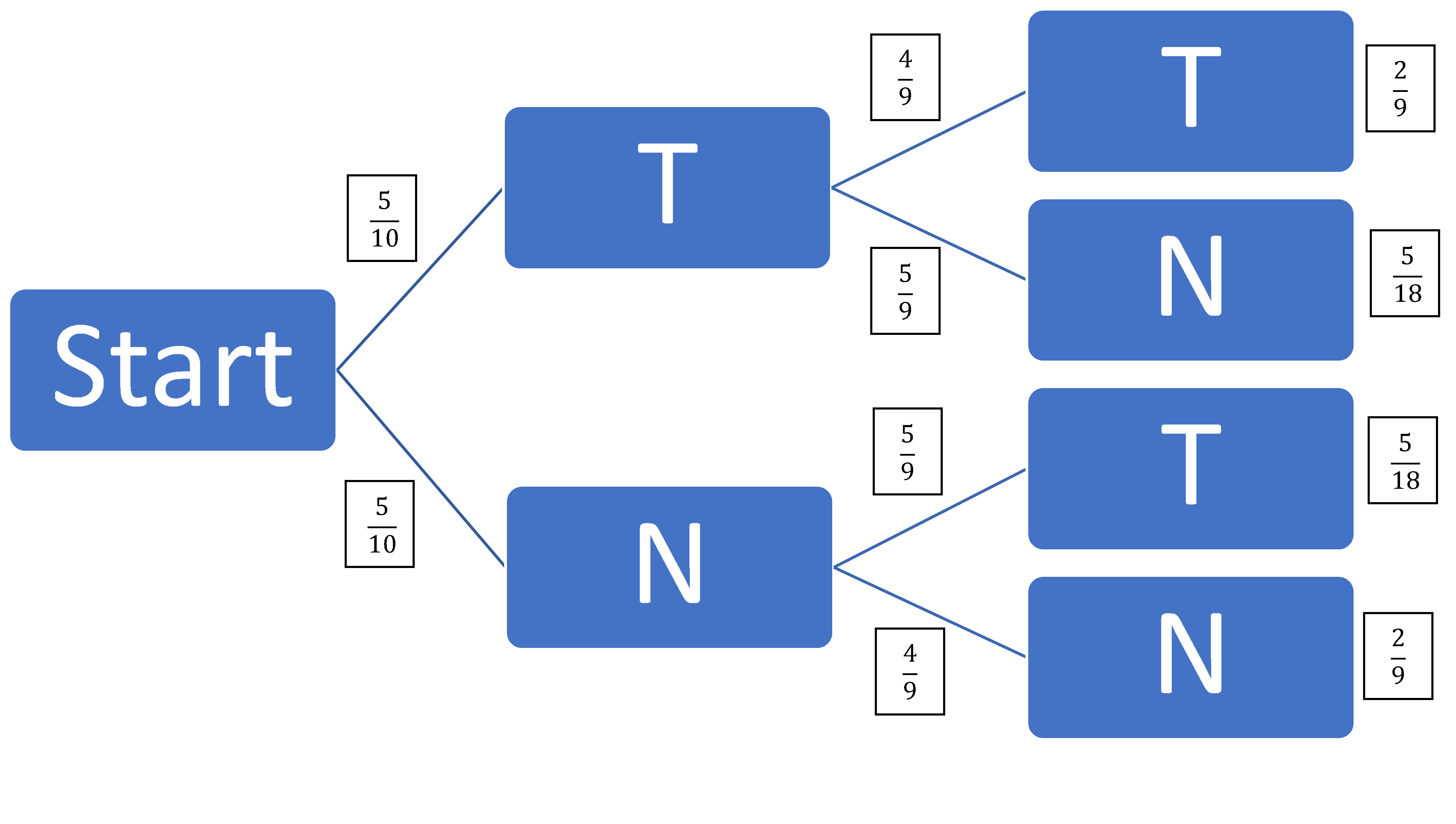
Dies ist ein Beispiel für ein Baumdiagramm für das zweimalige Ziehen von Losen ohne zurücklegen, es gibt 10 Lose, von denen 5 Treffer sind.