Beugung und Interferenz am Kristallgitter

Quantenmechanische Teilchen wie Photonen oder Elektronen lassen sich an einem Kristallgitter beugen / brechen, falls ihre Wellenlänge dies erlaubt.

Elektronenbeugungsröhre

Quelle: Finn-Pauls, Elektronenbeugungsröhre-Aufbau, CC BY 3.0

Auf dem Leuchtschirm können konzentrische Beugungsringe beobachtet werden, wobei die Interferenz auf die Bragg-Bedingung zurückzuführen ist.

$$\sin\left( \theta \right) = \frac{0,5\delta}{d}$$

$$\delta = \mathrm{\Delta}s = 2d \times sin(\theta)$$

Bedingung konstruktive Interferenz: $\mathrm{\Delta}s = \text{λk}$

Bedingung destruktive Interferenz:
$\mathrm{\Delta}s = \lambda(k + 0,5)$

Weil die einzelnen Kristallite in alle Raumrichtungen orientiert sind, entstehen kreisförmige Maxima, wobei sich das Licht vom Kristall aus entlang eines Kegelmantels ausbreitet und die Schnittkreise mit dem Schirm als Maxima zu erkennen sind. Die Wellenlänge bei Quantenobjekten mit Masse ist die De-Broglie-Wellenlänge. Der Kristall ist polykristallin, er besteht aus vielen Einzelkristallen, es kann mehrere Netzabstände geben.

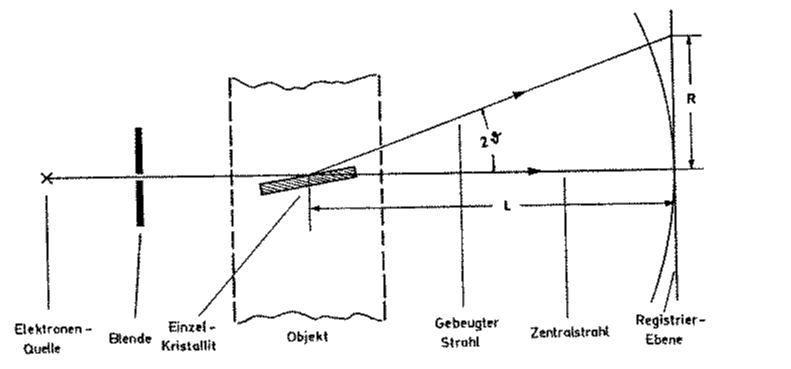
Außerdem gilt nach dieser Skizze bei folgender Anordnung:

Das Kristallgitter steht zusätzlich um den Reflexionswinkel schräg (Eintrittswinkel=Austrittswinkel), daher ist der Gesamtwinkel $2\theta_{k}$.

$$2\theta_{k} = Ablenkwinkel$$

$$\tan\left( 2\theta_{k} \right) = \frac{R_{k}}{L}$$

Um Elektronen und Photonen zu unterscheiden kann ein Magnet vor den Schirm platziert werden, durch die Lorentzkraft kommt es zu einem veränderten Bild bei Elektronen.

Auch ist über die Elektronenbeugungsröhre die Bestimmung von h möglich, da die De-Broglie Wellenlänge der Elektronen zum einen über die Beugungserscheinungen und zum anderen über die Beschleunigungsspannung und hieraus resultierende kinetische Energie berechnet werden kann.

Beim ersten Maximum gilt:

$$\lambda = 2d \times sin\left( \frac{1}{2}arctan\left( \frac{R_{k}}{L} \right) \right)$$

$$\lambda = \frac{h}{\text{mv}} = \frac{h}{m \cdot \sqrt{\frac{2eU}{m}}} = \frac{h}{\sqrt{2eUm}}$$

Graphisch kann zudem $\lambda$ über $\frac{1}{\sqrt{2eUm}}$ (insgesamt ist die Methode so darzustellen wichtig) aufgetragen werden, wobei h dann die Steigung ist.

Senkrechtes Auftreffen auf eine Kristallschicht

Treffen zwei Strähle parallel und senkrecht auf eine Kristallschicht und werden abgelenkt, so ergibt sich folgendes Bild.

Daraus folgt: 

$$\cos\left( 90{^\circ} - \alpha \right) = \frac{\mathrm{\Delta}s}{d}$$

$$\mathrm{\Delta}s = sin(\alpha) \cdot d$$