Physik → Atomphysik →

Compton-Effekt

Der Compton-Effekt beschreibt die Vergrößerung der Wellenlänge eines Photons bei der Streuung an einem Teilchen (z. B. Elektron). Wie der Photoeffekt unterstreicht der Compton-Effekt die Teilcheneigenschaften des Lichts, denn nach der klassischen Wellentheorie müsste die Welle durch ihr elektromagnetisches Feld Elektronenschwingungen auslösen, welche wiederum für eine Welle gleicher Frequenz sorgen müssten.

undefined

Quelle: EoD, Compton scattering-de, CC BY-SA 3.0

Bei dem vollelastischen^[1] Zusammenstoß verliert das Photon an Energie, die Wellenlänge wird je nach Winkel um $\Delta\lambda$ vergrößert. Für $\Delta\lambda$ gilt:

Δ λ = \frac{h}{m \cdot c} (1 - c o s (φ))

$\Delta\lambda = \frac{h}{m \cdot c}\left( 1 - cos(\varphi) \right)$

$m$ ist hierbei die Masse des Teilchens, auf welches das Photon trifft.

Erklärung zur Grafik

Der Strich in der Mitte symbolisiert den Impulspfeil des Photons, welcher über seine Länge den Impuls dieses vor dem Zusammenstoß und über die Richtung die Richtung des vorherigen Impulses (entlang der normalen Flugbahn) veranschaulicht. Die nach dem Zusammenstoß bestehenden Impulspfeile müssen zusammen wieder dem mittleren entsprechen (analog zum Kräfteparallelogramm).

Aufgrund der geringen Größe der Wellenlängendifferenz macht sich der Effekt besonders bei kurzwelliger elektromagnetischer Strahlung (z. B. Röntgen bemerkbar) und ist zum Beispiel bei sichtbarem Licht zu gering, um wahrgenommen zu werden.

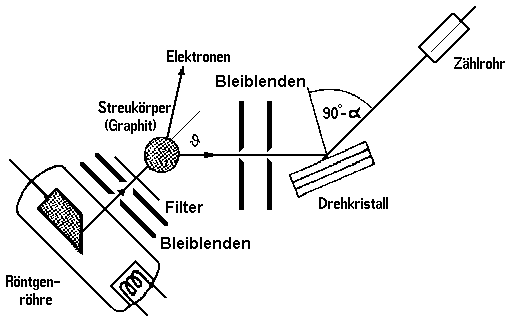
Comptons Versuch

undefined

Quelle

Über den Drehkristall kann eine Intensitätsverteilung über die Wellenlänge aufgenommen werden. Bei weiter innen im Atom liegenden Elektronen kann aufgrund der starken Bindung dieser fast keine Energie beim Stoß abgegeben werden, die ursprüngliche Wellenlänge bleibt bei diesen Zusammenstößen so gut wie erhalten. So ergibt sich folgenden Intensitätsverteilung:

undefined

Quelle

$\mathrm{\Delta}\lambda$ ist hierbei vom Material des Streukörpers unabhängig, da es immer zu dem Stoß mit fast freien Elektronen kommt. Je höher die Ordnungszahl, desto mehr Elektronen sind fest gebunden und desto höher ist der Anteil der verlustfrei reflektierten Strahlung. Mit steigendem $\vartheta$ steigt auch $\mathrm{\Delta}\lambda$ .

Zusammenfassung der Beobachtungen

In der Streustrahlung tritt neben $\lambda$ die größere Wellenlänge $\lambda + \Delta\lambda$ auf.
$\Delta\lambda$ steigt mit zunehmendem Streuwinkel $\vartheta$
Mit zunehmendem $\vartheta$ nimmt die Intensität der langwelligeren Streustrahlung auf Kosten der kurzwelligeren ab.
Je Höher die Ordnungszahl des Elements, desto geringer der Anteil der Streustrahlung mit längerer Wellenlänge.
$\Delta\lambda$ ist materialunabhängig

Herleitung

Im Folgenden wird von einem ruhenden freien Elektron ausgegangen. Ziel ist, die durch den Compton-Effekt verursachte Wellenlängenverschiebung zu bestimmen.

Energien und Impulse der Teilchen beim Compton-Effekt

Energie des Elektrons vorher	Energie des Photons vorher	Impuls des Photons vorher	Impuls des Elektrons vorher
$E_{e} = m_{0} \cdot c^{2}$	$E_{p} = h \cdot f$	$p_{p} = \frac{h \cdot f}{c}$	$p_{e} = 0$
Energie des Elektrons nachher	Energie des Photons nachher	Impuls des Photons nachher	Impuls des Elektrons nachher
$E_{e}^{`}$	$E_{p}^{`} = h \cdot f´$	$p_{p}^{`} = \frac{h \cdot f´}{c}$	$p_{e}^{`}$

Benötigte Zusammenhänge

Energie- und Impulserhaltungssatz

Es handelt sich um einen elastischen Stoß, der Energie- und Impulserhaltungssatz müssen erfüllt sein.

Energieerhaltungssatz	Impulserhaltungssatz
$E_{e} + E_{p} = E_{e}^{`} + E_{p}^{`}$	$p_{p} + p_{e} = p_{p}^{`} + p_{e}^{`}$

Hierüber kann ein Zusammenhang für $E_{e}^{`}$ aufgestellt werden.

E_{e}^{‘} = E_{p} - E_{p}^{‘} + E_{e} = h \cdot f - h \cdot f ´ + m_{0} \cdot c^{2}

$E_{e}^{`} = E_{p} - E_{p}^{`} + E_{e} = h \cdot f - h \cdot f´ + m_{0} \cdot c^{2}$

Relativistische Energie-Impuls-Beziehung

Auch gilt die relativistische Energie-Impuls-Beziehung.

Relativistische Energie-Impuls-Beziehung

Übertragen auf das freie Elektron

E^{2} = E_{0}^{2} + {(c \cdot p)}^{2}

$E^{2} = E_{0}^{2} + \left( c \cdot p \right)^{2}$

E_{0}^{2} = E^{2} - {(c \cdot p)}^{2}

$E_{0}^{2} = E^{2} - \left( c \cdot p \right)^{2}$

E_{e}^{2} = {E_{e}^{‘}}^{2} - {{p_{e}^{‘}}^{2} \cdot c}^{2}

$E_{e}^{2} = {E_{e}^{`}}^{2} - {{p_{e}^{`}}^{2} \cdot c}^{2}$

Für die Herleitung siehe Energie-Impuls-Beziehung.

Kosinussatz

Allgemein

Quelle: Petr K,Triangle - angles, vertices, sides,CC BY-SA 3.0

c^{2} = a^{2} + b^{2} - 2 \cdot a \cdot b \cdot c o s (γ)

$c^{2} = a^{2} + b^{2} - 2 \cdot a \cdot b \cdot cos(\gamma)$

Übertragen auf den Compton-Effekt

Quelle

$p_{\gamma}$ in der Grafik entspricht $p_{p}$ in den Gleichungen.

{p_{e}^{‘}}^{2} = p_{p}^{2} + {p_{p}^{‘}}^{2} - 2 \cdot p_{p} \cdot p_{p}^{‘} \cdot c o s (ϑ)

${p_{e}^{`}}^{2} = p_{p}^{2} + {p_{p}^{`}}^{2} - 2 \cdot p_{p} \cdot p_{p}^{`} \cdot cos(\vartheta)$

Verbinden der Zusammenhänge

Folgende ermittelte Zusammenhänge werden benötigt:

Zusammenhang aus der Energie- und Impulserhaltung (1)	Zusammenhang aus der Energie-Impuls-Beziehung (2)	Zusammenhang aus dem Kosinussatz (3)
$E_{e}^{`} = h \cdot f - h \cdot f´ + m_{0} \cdot c^{2}$	$E_{e}^{2} = {E_{e}^{`}}^{2} - {{p_{e}^{`}}^{2} \cdot c}^{2}$	${p_{e}^{`}}^{2} = p_{p}^{2} + {p_{p}^{`}}^{2} - 2 \cdot p_{p} \cdot p_{p}^{`} \cdot cos(\vartheta)$

1 und 3 werden in 2 eingesetzt.

E_{e}^{2} = {(h \cdot (f - f ´) + m_{0} \cdot c^{2})}^{2} - {(p_{p}^{2} + {p_{p}^{‘}}^{2} - 2 \cdot p_{p} \cdot p_{p}^{‘} \cdot c o s (ϑ)) \cdot c}^{2}

$E_{e}^{2} = \left( h \cdot \left( f - f´ \right) + m_{0} \cdot c^{2} \right)^{2} - {\left( p_{p}^{2} + {p_{p}^{`}}^{2} - 2 \cdot p_{p} \cdot p_{p}^{`} \cdot cos(\vartheta) \right) \cdot c}^{2}$

Zusätzlich werden die Zusammenhänge für die Impulse aus der Tabelle eingesetzt.

E_{e}^{2} = {(h \cdot (f - f ´) + m_{0} \cdot c^{2})}^{2} - {(\frac{{(h \cdot f)}^{2}}{c^{2}} + \frac{{(h \cdot f ´)}^{2}}{c^{2}} - 2 \cdot \frac{h^{2} \cdot f \cdot f ´}{c^{2}} \cdot c o s (ϑ)) \cdot c}^{2}

$E_{e}^{2} = \left( h \cdot \left( f - f´ \right) + m_{0} \cdot c^{2} \right)^{2} - {\left( \frac{\left( h \cdot f \right)^{2}}{c^{2}} + \frac{\left( h \cdot f´ \right)^{2}}{c^{2}} - 2 \cdot \frac{h^{2} \cdot f \cdot f´}{c^{2}} \cdot cos(\vartheta) \right) \cdot c}^{2}$

Nun wird ausmultipliziert und aufgelöst.

E_{e}^{2} = {(h \cdot (f - f ´) + m_{0} \cdot c^{2})}^{2} - ({(h \cdot f)}^{2} + {(h \cdot f ´)}^{2} - 2 \cdot h^{2} \cdot f \cdot f ´ \cdot c o s (ϑ))

$E_{e}^{2} = \left( h \cdot \left( f - f´ \right) + m_{0} \cdot c^{2} \right)^{2} - \left( \left( h \cdot f \right)^{2} + \left( h \cdot f´ \right)^{2} - 2 \cdot h^{2} \cdot f \cdot f´ \cdot cos(\vartheta) \right)$

E_{e}^{2} = {(h \cdot (f - f ´) + m_{0} \cdot c^{2})}^{2} - {(h \cdot f)}^{2} - {(h \cdot f ´)}^{2} + 2 \cdot h^{2} \cdot f \cdot f ´ \cdot c o s (ϑ)

$E_{e}^{2} = \left( h \cdot \left( f - f´ \right) + m_{0} \cdot c^{2} \right)^{2} - \left( h \cdot f \right)^{2} - \left( h \cdot f´ \right)^{2} + 2 \cdot h^{2} \cdot f \cdot f´ \cdot cos(\vartheta)$

E_{e}^{2} = h^{2} \cdot (f^{2} - 2 \cdot f \cdot f ´ + {f ´}^{2}) + 2 \cdot h \cdot (f - f ´) \cdot m_{0} \cdot c^{2} + m_{0}^{2} \cdot c^{4} - {(h \cdot f)}^{2} - {(h \cdot f ´)}^{2} + 2 \cdot h^{2} \cdot f \cdot f ´ \cdot \cos (ϑ)

$E_{e}^{2} = h^{2} \cdot \left( f^{2} - 2 \cdot f \cdot f´ + {f´}^{2} \right) + 2 \cdot h \cdot \left( f - f´ \right) \cdot m_{0} \cdot c^{2} + m_{0}^{2} \cdot c^{4} - \left( h \cdot f \right)^{2} - \left( h \cdot f´ \right)^{2} + 2 \cdot h^{2} \cdot f \cdot f´ \cdot \cos\left( \vartheta \right)$

E_{e}^{2} = {(h \cdot f)}^{2} - 2 \cdot h^{2} \cdot f \cdot f ´ + {(h \cdot f ´)}^{2} + 2 \cdot h \cdot (f - f ´) \cdot m_{0} \cdot c^{2} + m_{0}^{2} \cdot c^{4} - {(h \cdot f)}^{2} - {(h \cdot f ´)}^{2} + 2 \cdot h^{2} \cdot f \cdot f ´ \cdot c o s (ϑ)

$E_{e}^{2} = \left( h \cdot f \right)^{2} - 2 \cdot h^{2} \cdot f \cdot f´ + \left( h \cdot f´ \right)^{2} + 2 \cdot h \cdot \left( f - f´ \right) \cdot m_{0} \cdot c^{2} + m_{0}^{2} \cdot c^{4} - \left( h \cdot f \right)^{2} - \left( h \cdot f´ \right)^{2} + 2 \cdot h^{2} \cdot f \cdot f´ \cdot cos(\vartheta)$

E_{e}^{2} = - 2 \cdot h^{2} \cdot f \cdot f ´ + 2 \cdot h \cdot (f - f ´) \cdot m_{0} \cdot c^{2} + m_{0}^{2} \cdot c^{4} + 2 \cdot h^{2} \cdot f \cdot f ´ \cdot c o s (ϑ)

$E_{e}^{2} = - 2 \cdot h^{2} \cdot f \cdot f´ + 2 \cdot h \cdot \left( f - f´ \right) \cdot m_{0} \cdot c^{2} + m_{0}^{2} \cdot c^{4} + 2 \cdot h^{2} \cdot f \cdot f´ \cdot cos(\vartheta)$

Es gilt:

E_{e} = m_{0} \cdot c^{2}

$E_{e} = m_{0} \cdot c^{2}$

Hieraus folgt:

0 = - 2 \cdot h^{2} \cdot f \cdot f ´ + 2 \cdot h \cdot (f - f ´) \cdot m_{0} \cdot c^{2} + 2 \cdot h^{2} \cdot f \cdot f ´ \cdot c o s (ϑ)

$0 = - 2 \cdot h^{2} \cdot f \cdot f´ + 2 \cdot h \cdot \left( f - f´ \right) \cdot m_{0} \cdot c^{2} + 2 \cdot h^{2} \cdot f \cdot f´ \cdot cos(\vartheta)$

0 = 2 \cdot h \cdot m_{0} \cdot c^{2} \cdot (f - f ´) + 2 \cdot h^{2} \cdot f \cdot f ´ \cdot c o s (ϑ) - 2 \cdot h^{2} \cdot f \cdot f ´

$0 = 2 \cdot h \cdot m_{0} \cdot c^{2} \cdot \left( f - f´ \right) + 2 \cdot h^{2} \cdot f \cdot f´ \cdot cos(\vartheta) - 2 \cdot h^{2} \cdot f \cdot f´$

2 \cdot h^{2} \cdot f \cdot f ´ - 2 \cdot h^{2} \cdot f \cdot f ´ \cdot c o s (ϑ) = 2 \cdot h \cdot m_{0} \cdot c^{2} \cdot (f - f ´)

$2 \cdot h^{2} \cdot f \cdot f´ - 2 \cdot h^{2} \cdot f \cdot f´ \cdot cos(\vartheta) = 2 \cdot h \cdot m_{0} \cdot c^{2} \cdot \left( f - f´ \right)$

2 \cdot h^{2} \cdot f \cdot f ´ \cdot (1 - c o s (ϑ)) = 2 \cdot h \cdot m_{0} \cdot c^{2} \cdot (f - f ´)

$2 \cdot h^{2} \cdot f \cdot f´ \cdot \left( 1 - cos(\vartheta) \right) = 2 \cdot h \cdot m_{0} \cdot c^{2} \cdot \left( f - f´ \right)$

h \cdot f \cdot f ´ \cdot (1 - c o s (ϑ)) = m_{0} \cdot c^{2} \cdot (f - f ´)

$h \cdot f \cdot f´ \cdot \left( 1 - cos(\vartheta) \right) = m_{0} \cdot c^{2} \cdot \left( f - f´ \right)$

h \cdot (1 - c o s (ϑ)) = m_{0} \cdot c^{2} \cdot \frac{f - f ´}{f \cdot f ´}

$h \cdot \left( 1 - cos(\vartheta) \right) = m_{0} \cdot c^{2} \cdot \frac{f - f´}{f \cdot f´}$

\frac{f - f ´}{f \cdot f ´} = \frac{f}{f \cdot f ´} - \frac{f ´}{f \cdot f ´} = \frac{1}{f ´} - \frac{1}{f}

$\frac{f - f´}{f \cdot f´} = \frac{f}{f \cdot f´} - \frac{f´}{f \cdot f´} = \frac{1}{f´} - \frac{1}{f}$

h \cdot (1 - c o s (ϑ)) = m_{0} \cdot c \cdot (\frac{c}{f ´} - \frac{c}{f})

$h \cdot \left( 1 - cos(\vartheta) \right) = m_{0} \cdot c \cdot \left( \frac{c}{f´} - \frac{c}{f} \right)$

Es gilt:

c = λ \cdot f

$c = \lambda \cdot f$

λ = \frac{c}{f}

$\lambda = \frac{c}{f}$

(\frac{c}{f ´} - \frac{c}{f}) = λ ´ - λ = Δ λ

$\left( \frac{c}{f´} - \frac{c}{f} \right) = \lambda´ - \lambda = \mathrm{\Delta}\lambda$

h \cdot (1 - c o s (ϑ)) = m_{0} \cdot c \cdot Δ λ

$h \cdot \left( 1 - cos(\vartheta) \right) = m_{0} \cdot c \cdot \mathrm{\Delta}\lambda$

Δ λ = \frac{h}{m_{0} \cdot c} \cdot (1 - c o s (ϑ))

$\mathrm{\Delta}\lambda = \frac{h}{m_{0} \cdot c} \cdot \left( 1 - cos(\vartheta) \right)$

Energieverteilung der Compton-Elektronen

undefined

^[1] Elastisch → keine Energieumwandlung

Empfehlungen

To do

Franck-Hertz-Versuch

Castellio - gemeinfreie Werke frei verfügbar

Stefan Zweigs Werke

Sie möchten mir einen Kaffee spendieren?

Anmerkungen oder sonstige Ideen und Vorschläge können Sie gern per Mail an info@lernzettel.org bzw. fehler@lernzettel.org senden.