Hypothesentests

Beim Hypothesen- oder Signifikanztest wird eine Hypothese (genannt Nullhypothese H₀) zur Trefferwahrscheinlichkeit bei einem Bernoulli-Experiment überprüft. Hierbei werden Bereiche festgelegt, in welchen die Hypothese als richtig beziehungsweise falsch angesehen wird (wobei auch Fehler möglich sind). Die Wahrscheinlichkeit des Ablehnungsbereichs ist höchstens das Signifikanzniveau α. Ist die Nullhypothese falsch, gilt die Alternative H₁. Die Irrtumswahrscheinlichkeit ist die Wahrscheinlichkeit der Ablehnungsbereiche (beziehungsweise des Ablehnungsbereichs). Über die Sigmaregeln und Berechnen der kumulierten Wahrscheinlichkeit lässt sich der Annahmebereich (und somit der / die Ablehnungsbereich(e)) feststellen.

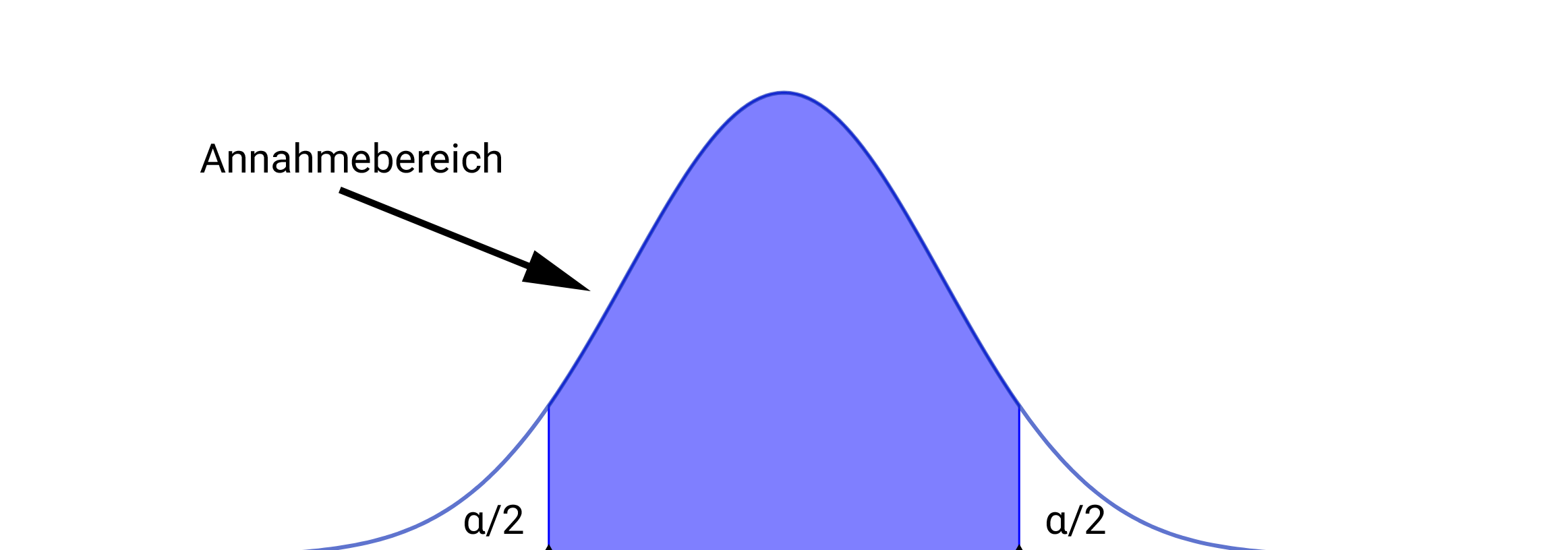
Zweiseitiger Signifikanztest

Beim Zweiseitigen Signifikanztest gibt es auf beiden Seiten Ablehnungsbereiche, von denen jeder maximal halb so wahrscheinlich wie das Signifikanzniveau sein darf.

Vorgehen

1. Es ist eine zu überprüfende Wahrscheinlichkeit für eine binomialverteilte Zufallsgröße, sowie n und das Signifikanzniveau gegeben, wobei das Ziel ist, Bereiche festzulegen, in welchen die Hypothese unter diesem Signifikanzniveau als richtig oder falsch angenommen wird. So stellt man folgendes auf:
   $$H_{0}:p = p_{0}$$
   $$H_{1}:p \neq p_{0}$$

2. Nun wird nach den Sigmaregeln eine Näherung vorgenommen. Bei einem Signifikanzniveau von 5% würde so das 1,96σ-Intervall genommen werden, über welches sich ein Annahmebereich ergibt. Aus diesem Annahmebereich ergeben sich dann Ablehnungsbereiche, welche im Folgenden überprüft werden. Bei einem Annahmebereich von 20-30 bei n=50, wären die Ablehnungsbereiche somit 0-19 und 31-50.
3. Diese Ablehnungsbereiche werden im Folgenden überprüft (über die Formel zur kumulierten Binomialverteilung) und so festgelegt, dass die Wahrscheinlichkeit jeweils maximal dem halben Signifikanzniveau entspricht und so nah wie möglich an dieses herankommt.
4. Der Annahmebereich $\left\lbrack a;b \right\rbrack$ liegt dann zwischen den Ablehnungsbereichen.

Linksseitiger Test

Der Ablehnungsbereich befindet sich links der Annahmebereich ist $\left\lbrack a;n \right\rbrack$. Die Nullhypothese ist entweder $H_{0}:p = p_{0}$ oder $H_{0}:p \geq p_{0}$. Die Alternative ist $H_{1}:p < p_{0}$.

Vorgehen

Das Vorgehen entspricht dem beim zweiseitigen Test weitgehend. Allerdings ist darauf zu achten, dass das Signifikanzniveau nur auf einer Seite ist und somit ein anderes Sigma-Intervall zu wählen ist (bei 5% das 1,64-Sigma-Intervall). Der linke Ablehnungsbereich wird bestimmt, sodass dessen Wahrscheinlichkeit möglichst nah an das Signifikanzniveau kommt, der Annahmebereich fängt dann 1 nach dem Ende des Ablehnungsbereiches an.

Rechtsseitiger Test

Annahmebereich:
$\left\lbrack 0;b \right\rbrack$

Nullhypothese: $H_{0}:p = p_{0}$ oder $H_{0}:p \leq p_{0}$

Alternative: $H_{0}:p > p_{0}$

Der Ablehnungsbereich wird so bestimmt, dass dessen Wahrscheinlichkeit
möglichst nah an das Signifikanzniveau kommt.

Zusammenfassende Bedingungen

Es ergibt sich folgende Bedingung für die rechte Seite (rechtseitiger Test):

Gewählt wird der kleinste Wert b, für den gilt: $P(b + 1 \leq x \leq n) \leq \alpha$

Es ergibt sich folgende Bedingung für die linke Seite (linksseitiger Test):

Gewählt wird der größte Wert a, für den gilt: $P(x \leq a - 1) \leq \alpha$

Beim beidseitigen Test wird jeweils $\frac{\alpha}{2}$ verwendet.

Fehler beim Testen

Fehler 1. Art

Die Nullhypothese wurde abgelehnt, obwohl sie richtig ist. Die Wahrscheinlichkeit hierfür ist die Irrtumswahrscheinlichkeit, also die Wahrscheinlichkeit der Ablehnungsbereiche beziehungsweise die Gegenwahrscheinlichkeit des Annahmebereichs.

Fehler 2. Art

Die Nullhypothese wurde angenommen, obwohl sie falsch ist. Die Wahrscheinlichkeit hierzu hängt von der tatsächlichen Wahrscheinlichkeit des Versuches ab. Sie ist die tatsächliche Wahrscheinlichkeit für den Annahmebereich (unter Verwendung der tatsächlichen Wahrscheinlichkeit.

Der Fehler 2. Art wird durch eine Erhöhung des Signifikanzniveaus unwahrscheinlicher, wodurch allerdings der Fehler 1. Art wahrscheinlicher wird. Für bessere Ergebnisse wird der Stichprobenumfang erhöht.