Schnittwinkel in der analytischen Geometrie

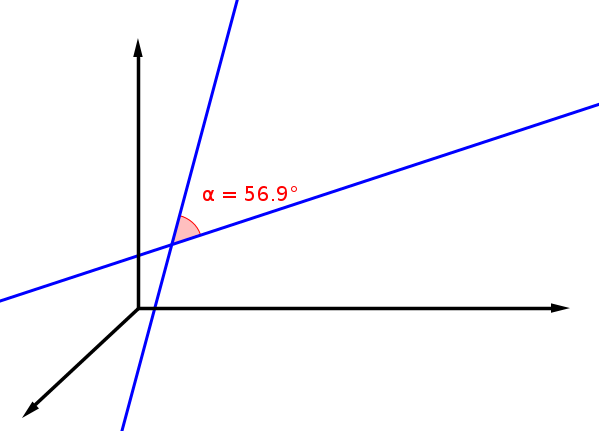
Schnittwinkel zweier Geraden

Wiederholung der Gerade-Gerade Lagebeziehungen

1. Identisch → Richtungsvektoren vielfache && erfüllte Punktprobe für alle Punkte
2. Parallel → nur Richtungsvektoren vielfache
3. Schnittpunkt → Gleichsetzen, Auflösen, Schnittpunkt ermittelbar, nicht gleich
4. Windschief → kein Schnittpunkt, nicht parallel

Quelle: Serlo

Hierbei sind u und v die Richtungsvektoren der Geraden.

Dies lässt sich vereinfacht aus der Definition des Skalarprodukts herleiten:

Das Skalarprodukt $\overrightarrow{u}{^\circ}\overrightarrow{v}$ ist definiert als:
$\overrightarrow{u}{^\circ}\overrightarrow{v} = \left| \overrightarrow{u} \right| \cdot \left| \overrightarrow{v} \right| \cdot cos(\alpha)$

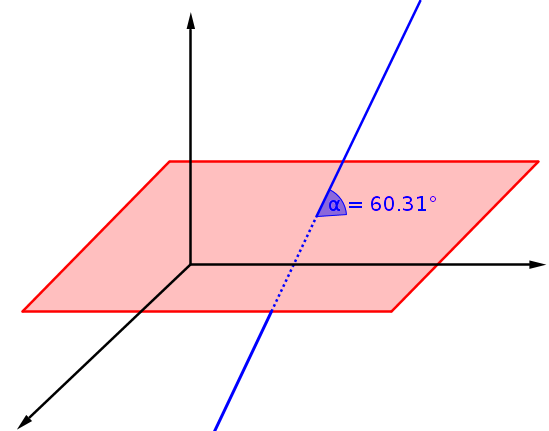
Schnittwinkel zwischen Ebene und Gerade

Schneidet eine Gerade eine Ebene in einem Schnittpunkt (siehe: Gegenseitige Lage von Geraden und Ebenen), so lässt sich auch hier der Schnittwinkel berechnen.

Quelle: Serlo

$\sin\left( \alpha \right) = \frac{\left| \overrightarrow{n}{^\circ}\overrightarrow{u} \right|}{\left| \overrightarrow{n} \right| \cdot \left| \overrightarrow{u} \right|}$

Hierbei ist n der Normalenvektor der Ebene und u der Richtungsvektor der Gerade.

Herleitung: Der Schnittwinkel zwischen der Ebene und der Gerade ist 90° minus der Schnittwinkel aus Normale der Ebene und Gerade. Daher gilt nach der obigen Herleitung:
$\cos\left( 90 - \alpha \right) = \frac{\left| \overrightarrow{n}{^\circ}\overrightarrow{u} \right|}{\left| \overrightarrow{n} \right| \cdot \left| \overrightarrow{u} \right|}$,
beziehungsweise
$\sin\left( \alpha \right) = \frac{\left| \overrightarrow{n}{^\circ}\overrightarrow{u} \right|}{\left| \overrightarrow{n} \right| \cdot \left| \overrightarrow{u} \right|}$.

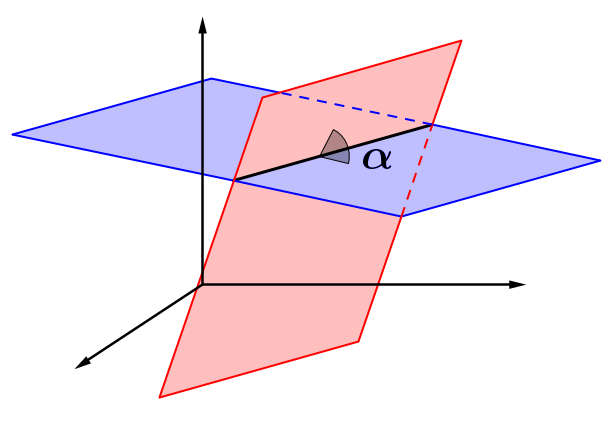
Schnittwinkel zweier Ebenen

Quelle: Serlo

Ebenen können sich in einer Schnittgeraden schneiden. Da die Normalen einen festen Winkel zu ihrer Ebene besitzen (90°), entspricht ihr Schnittwinkel (der der Normalen der Ebenen) dem der Ebenen. Somit gilt:
$\cos\left( \alpha \right) = \frac{\left| \overrightarrow{n}{^\circ}\overrightarrow{m} \right|}{\left| \overrightarrow{n} \right| \cdot \left| \overrightarrow{m} \right|}$,
wobei n und m die Normalenvektoren der Ebenen sind.