Analysis Zusammenfassung Abitur

Themen

Bestimmung von Nullstellen
- Mitternachtsformel
- Ausklammern
- Substituieren
Kenntnisse zu bestimmten Funktionen (Verlauf und Definitionsbereich)
- e
- ln
- trigonometrische Funktionen
Ableiten
- Ableitungsregeln
- Ableiten von bestimmten Funktionen
Kurvendiskussion
- Nullstellen
- Extremstellen
- Wendestellen
- Symmetrie
- Monotonie
Tangentengleichungen
Normalengleichungen
Integrale
- Integrale allgemein
- Stammfunktionen ermitteln
- Partielle Integration
- Integration durch Substitution
- Uneigentliche Integrale
- Fläche zwischen zwei Graphen
  - Differenzfunktion
  - Zwischen Funktionen und Achsen
- Rotationskörper
Abstandsberechnungen
- Pythagoras

Bestimmung von Nullstellen

Um die Schnittpunkte einer Funktion mit der x-Achse zu bestimmen, können mehrere Verfahren genutzt werden.

Mitternachtsformel

Bei ganzrationalen Funktionen zweiten Grades ( $f\left( x \right) = ax^{2} + bx + c$ ) kann die Mitternachtsformel verwendet werden.

x_{1 / 2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

$x_{1/2} = \frac{- b \pm \sqrt{b^{2} - 4ac}}{2a}$

Ausklammern

Eine Gleichung wird immer dann 0, wenn einer der Faktoren 0 ist. Durch Ausklammern können häufig einfach lösbare Faktoren erreicht werden.

Substituieren

Liegt eine Funktion nach dem Muster $f\left( x \right) = ax^{4} + bx^{2}$ vor, so kann durch $z = x^{2}$ folgende mit der Mitternachtsformel lösbare Funktion erzeugt werden:

a z^{2} + b z

$az^{2} + bz$

Für die letztendliche Lösung muss dann aus dem Ergebnis wieder die Wurzel gezogen werden, wobei zu beachten ist, dass es sowohl eine negative als auch eine positive Lösung gibt.

Taschenrechner

Die Bestimmung von Nullstellen ist ein Basiskonzept, welches in der Berechnung über diese Methoden im Teil ohne Hilfsmittel von Nöten sein könnte. Ansonsten ist es deutlich effizienter, den Taschenrechner zu nutzen. Beim Casio fx-991DEX unter Mode → A → 2.

Kenntnisse zu bestimmten Funktionen

e-Funktion

Bei der e-Funktion ( $e^{x}$ ) handelt es sich um eine Exponentialfunktion, welche im Gegensatz zur Potenzfunktion die Variable im Exponenten hat. Besonders an der e-Funktion ist, dass ihre Ableitung wieder die e-Funktion ist. Ihr Graph heißt Exponentialkurve und sieht folgendermaßen aus:

undefined

es existiert kein Schnittpunkt mit der x-Achse – keine Nullstelle

e ist die Eulersche Zahl, ist irrational und beträgt circa 2,718

Lösung der e-Funktion

Wiederholung zum Logarithmus

b^{x} = a

$b^{x} = a$

x = \log_{b} (a)

$x = \log_{b}(a)$

Der natürliche Logarithmus

e^{x} = z

$e^{x} = z$

x = l n (z)

$x = ln(z)$

ln-Funktion

Die Lösung des natürlichen Logarithmus lässt sich auch als Funktion darstellen, $f\left( x \right) = ln(x)$ .

undefined

da $e^{x}$ niemals 0 oder negativ sein kann (zumindest bei reellen Zahlen), ist der natürliche Logarithmus hier nicht definiert

Trigonometrische Funktionen

Sinus

undefined

Der Graph kann verändert werden:

$f\left( x \right) = a \cdot \sin\left( b \cdot \left( x - c \right) \right) + d$

a = A m p l i t u d e

$a = Amplitude$

$b = Periodenlänge$ (wobei die ursprüngliche Periodenlänge von 2π durch diesen Wert geteilt wird)

c = V e r s c h i e b u n g a u f d e r x - A c h s e

$c = Verschiebung\ auf\ der\ x - Achse$

d = V e r s c h i e b u n g a u f d e r y - A c h s e

$d = Verschiebung\ auf\ der\ y - Achse$

Insgesamt erinnert dies an die Scheitelpunktform einer Funktion.

Nullstellen	Größte Funktionswerte	Kleinste Funktionswerte
$x = k \cdot \pi$	$x = \frac{1}{2}\pi + k \cdot 2\pi$	$x = \frac{3}{2}\pi + k \cdot 2\pi$

Cosinus

Der Cosinus (im Bild blau) ist eine um 1/2𝛑 nach links verschobene Sinuskurve.

undefined

Nullstellen	Größte Funktionswerte	Kleinste Funktionswerte
$x = \frac{1}{2}\pi + k \cdot \pi$	$x = k \cdot 2\pi$	$x = \pi + k \cdot 2\pi$

Ableiten

Mit der Ableitung wird eine Funktion erzeugt, welche an allen Stellen die Steigung der ursprünglichen Funktion zeigt. Der weitere Nutzen von Ableitungen wird unter Kurvendiskussion ersichtlich.

Ableitungsregeln

Seien f, g und h differenzierbare, reelle Funktionen, n und a reelle Zahlen, dann gilt:

Konstante Funktionen

(a) ´ = 0

$\left( a \right)´ = 0$

Potenzregel

(x^{n}) ´ = n x^{n - 1}

$\left( x^{n} \right)´ = nx^{n - 1}$

Faktorregel

(a \cdot f) ´ = a \cdot f ´

$\left( a \cdot f \right)´ = a \cdot f´$

Summenregel

(g \pm h) ´ = g ´ \pm h ´

$\left( g \pm h \right)´ = g´ \pm h´$

Kettenregel

(g \circ h) ´ (x) = (g (h (x)) ´ = g ´ (h (x)) \cdot h ´ (x)

$\left( g \circ h \right)´\left( x \right) = (g\left( h\left( x \right) \right)´ = g´(h\left( x \right)) \cdot h´(x)$

Produktregel

(g \cdot h) ´ = g ´ \cdot h + g \cdot h ´

$\left( g \cdot h \right)´ = g´ \cdot h + g \cdot h´$

Quotientenregel

(\frac{g}{h}) ´ = \frac{g ´ \cdot h - g \cdot h ´}{h^{2}}

$\left( \frac{g}{h} \right)´ = \frac{g´ \cdot h - g \cdot h´}{h^{2}}$

Ableiten der e-Funktion

Die e-Funktion wird nach der Kettenregel abgeleitet, wobei die Ableitung der äußeren Funktion $e^{x}$ wieder $e^{x}$ ist.

Beispiel: $f\left( x \right) = e^{2x^{2} + 3}$
$f´\left( x \right) = 4x \cdot e^{2x^{2} + 3}$

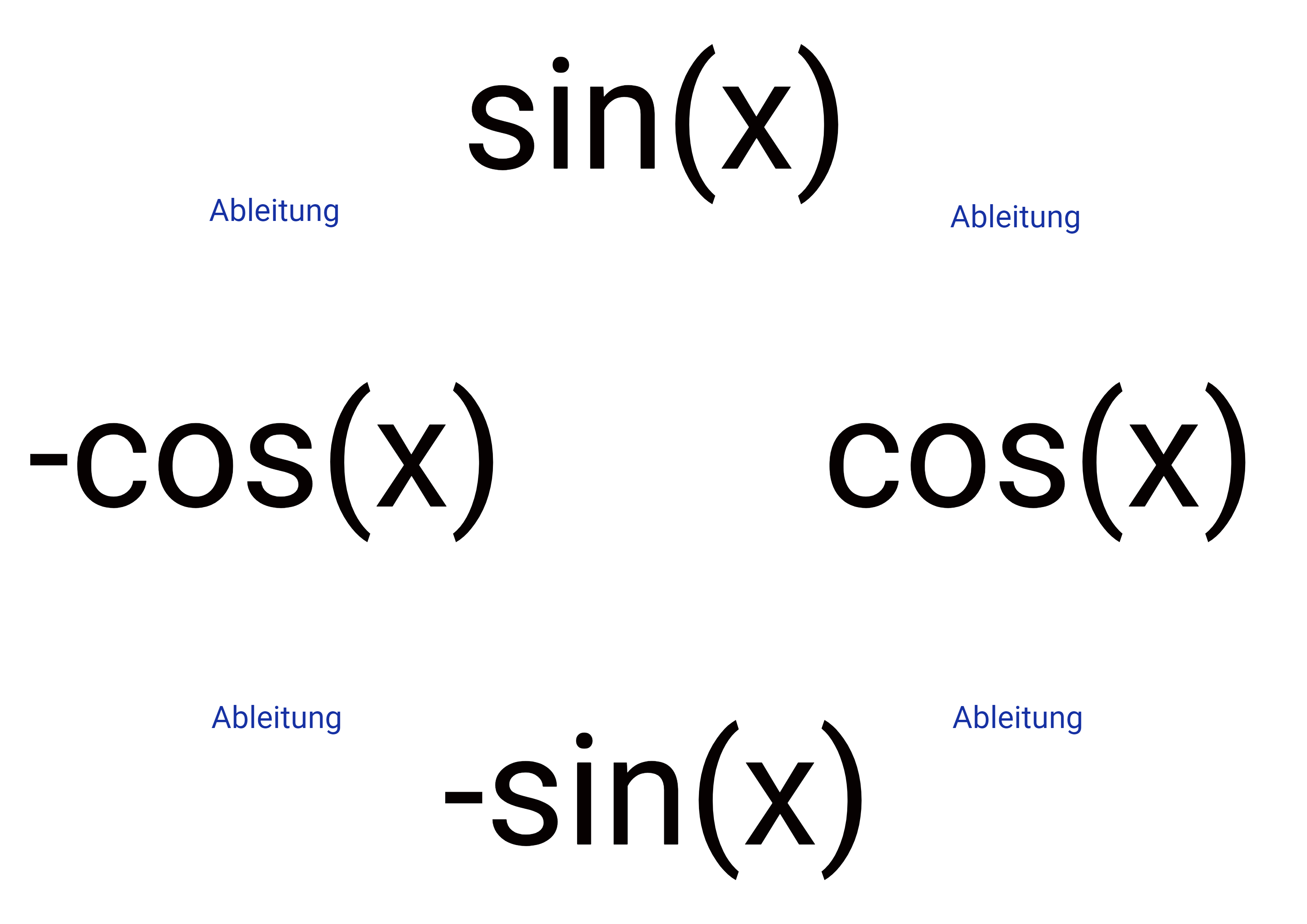
Ableiten der trigonometrischen Funktion

Auch hier wird nach der Kettenregel abgeleitet, wobei für die äußere Funktion gilt (gelesen im Uhrzeigersinn):

ableitung-sinus-cosinus.svg.png

Beispiel: $f\left( x \right) = sin(2x)$ $f´\left( x \right) = 2 \cdot cos(2x)$

Kurvendiskussion

Definitionsbereich bestimmen

Der maximale Definitionsbereich wird gesucht, also der Bereich, in welchem die Funktion berechnet werden kann.

Folgende Definitionsbereiche sind möglich:

N = {0, 1, 2, 3...} (n a t ü r l i c h e Z a h l e n)

$N = \left\{ 0,1,2,3... \right\}\ (natürliche\ Zahlen)$

Z = {. . . - 3, - 2, - 1, 0, 1, 2, 3...} (g a n z e Z a h l e n)

$Z = \left\{ ... - 3, - 2, - 1,0,1,2,3... \right\}\ (ganze\ Zahlen)$

Q = {m n | m, n \in Z, n \neq 0} (r a t i o n a l e Z a h l e n)

$Q = \{ mn\ |\ m,\ n \in Z,n \neq 0\}(rationale\ Zahlen)$

R (a l l e r e e l l e n Z a h l e n (a l l e s b i s a u f i m a g i n ä r e Z a h l e n))

$R(alle\ reellen\ Zahlen\ (alles\ bis\ auf\ imaginäre\ Zahlen))$

Der Definitionsbereich lässt sich folgendermaßen einschränken:

R^{+} (n u r p o s i t i v e Z a h l e n)

$R^{+}(nur\ positive\ Zahlen)$

R^{-} (n u r n e g a t i v e Z a h l e n)

$R^{-}(nur\ negative\ \ Zahlen)$

R_{0}^{+} (n u r p o s i t i v e Z a h l e n u n d d i e 0)

$R_{0}^{+}\ (nur\ positive\ Zahlen\ und\ die\ 0)$

R ∖ {0; 2} (r e e l l e Z a h l e n b i s a u f 0 u n d 2)

$R\backslash\{ 0;2\}(reelle\ Zahlen\ bis\ auf\ 0\ und\ 2)$

Beispiel:

f (x) = \frac{1}{x}

$f(x) = \frac{1}{x}$

Da 0 nicht im Nenner stehen darf, gilt: $D = R\backslash\{ 0\}$

Nullstellen bestimmen

Bei linearen Funktionen wird die Funktion gleich 0 gesetzt und dann zu x umgestellt. Bei Quadratischen Funktionen nutzt man die Mitternachtsformel (siehe AB). Insgesamt gilt, dass der Term gleich null ist, wenn einer der Faktoren oder der Zähler null ist.

Symmetrie bestimmen

Punktsymmetrie zum Ursprung

Es gilt: $f( - x) = - f(x)$ , also wenn alle Exponenten ungerade sind.

Achsensymmetrie zur y-Achse

Es gilt: $f( - x) = f(x)$ , also wenn alle Exponenten gerade sind.

Schnittstellen mit der y-Achse

Für x wird 0 eingesetzt, mögliche Schnittpunkte werden berechnet.

Da die Definitionsmenge des natürlichen Logarithmus $D = \rbrack 0;\infty\lbrack$ ist, ist die Stelle $x = 0$ nicht definiert, es gibt keine Schnittstelle.

Verhalten gegen unendlich

Wie verhält sich die Funktion bei unendlich hohen bzw. niedrigen x-Werten?

Es gilt:

der höchste Exponent entscheidet, bei geraden Exponenten ist das Ergebnis positiv, bei ungeraden Exponenten wird der Vorfaktor (also +/-) nicht verändert.

Extrempunkte

An Extrempunkten entspricht der Wert der ersten Ableitung null. Wir leiten ab, finden die Nullstellen der ersten Ableitung und gehen dann so vor:

Bei einem Hochpunkt ist der Wert der zweiten Ableitung an der Nullstelle der ersten Ableitung größer als null, bei Tiefpunkten ist dieser kleiner als null.

Es kann auch die Steigung kurz vor und nach dem Extrempunkt betrachtet werden:

+ \to - = H o c h p u n k t

$+ \ \rightarrow \ - \ = Hochpunkt$

- \to + = T i e f p u n k t

$- \ \rightarrow + \ = Tiefpunkt$

Sattelpunkte

Bei Sattelpunkten gilt:

f ´ (x) = 0

$f´(x) = 0$

f ´ ´ (x) = 0

$f´´(x) = 0$

f ´ ´ ´ (x) \neq 0

$f´´´(x) \neq 0$

Es kann auch die Steigung kurz vor und nach der Nullstelle der 1. Ableitung betrachtet werden, gibt es keinen Vorzeichenwechsel handelt es sich um einen Sattelpunkt.

Wendepunkte

Man sucht die Nullstellen der zweiten Ableitung und setzt diese in die dritte Ableitung ein. Ist der Wert ungleich null, gibt es hier einen Wendepunkt, also ein Maximum ein dem Graphen der ersten Ableitung.

Ein Wendepunkt ist sozusagen ein ,,Schlenker” im Graphen, also ein Richtungswechsel.

Monotonieverhalten

Zuerst werden die Extremstellen berechnet.

Hochpunkt → Tiefpunkt = streng monoton fallend

Tiefpunkt → Hochpunkt = streng monoton steigend

Bei den äußeren Extremstellen gilt:

Tiefpunkt = streng monoton fallend bis zum Tiefpunkt, danach steigend

Hochpunkt = streng monoton steigend bis zum Hochpunkt, danach fallend

Tangentengleichung

y = m x + b

$y = mx + b$

m = f ´ (x)

$m = f´(x)$

Dann werden der x- und y-Wert der ursprünglichen Funktion eingesetzt und die Gleichung berechnet.

Normalengleichung

Die Normale steht senkrecht zur Tangente, ihre Steigung ist $m_{n} = - \frac{1}{m}_{t}$ .

Gegebenen Punkt (oft muss der y-Wert durch Einsetzen des x-Wertes in die ursprüngliche Funktion ermittelt werden) und den gewonnenen Wert für m in die Gleichung

y = m x + b

$y = mx + b$ einsetzen und b ermitteln - schon ist die lineare Gleichung bestimmt.

Integrale

Geht man von einer stetigen Funktion F aus, so zeigt die Ableitung f an jeder Stelle die Steigung der ursprünglichen Funktion. Hieraus folgt, dass die Fläche, welche der Graph von f mit der x-Achse in einem Intervall aufspannt, dem Höhenunterschied von F in diesem Intervall entspricht.

Beispiel:

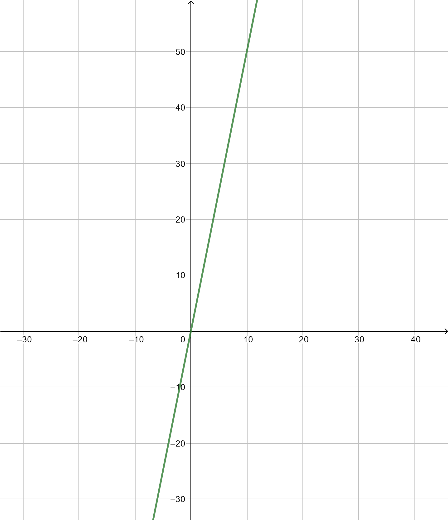
Ein Läufer läuft 10 Stunden mit 5 km/h. Für den Graphen der Strecke ergibt sich folgendes:

undefined

Nach 10 Stunden wurden 50km erreicht. Die Ableitung der Funktion des Weges ist die Geschwindigkeit, welche Konstant bei 5km/h liegt. Die von dem Graphen der Geschwindigkeit aufgespannte Fläche ist $5\frac{\text{km}}{h} \times 10h = 50km$ und somit dem Höhenunterschied in dem Graphen des Weges entsprechend.

Diese Eigenschaft kann man sich zu Nutzen machen, um die von einem Graphen in einem Intervall aufgespannte Fläche zu bestimmen.

Die Fläche kann auch berechnet werden, indem in die Fläche Rechtecke mit einer Breite gegen 0 platziert werden, und deren Flächen summiert werden.

A = Δ x \times f (x_{0}) + Δ x \times f (x_{1}) + \dots | Δ x \to 0

$A = \mathrm{\Delta}x \times f\left( x_{0} \right) + \mathrm{\Delta}x \times f\left( x_{1} \right) + \ldots|\ \mathrm{\Delta}x \rightarrow 0$

Um dies auszudrücken, wird folgende Schreibweise des Integrals verwendet:

\int_{a}^{b} f (x) dx

$\int_{a}^{b}{f\left( x \right)\text{dx}}$

Aus der Einleitung folgt, dass

\int_{a}^{b} f (x) d x = [F (x)] \begin{matrix} b \\ a \end{matrix} = F (b) - F (a)

$\int_{a}^{b}{f\left( x \right)dx = \left\lbrack F(x) \right\rbrack\begin{matrix} b \\ a \\ \end{matrix} = F\left( b \right) - F(a)}$

Wobei der berechnete Flächeninhalt der orientierte Flächeninhalt ist. Dies bedeutet, dass Flächen unter der x-Achse im Integral von der Gesamtfläche abgezogen werden.

Aus der Formel ergibt sich, dass es zur Berechnung des Flächeninhaltes eine Stammfunktion F braucht, zu welcher f eine mögliche Ableitung ist.

Finden einer Stammfunktion

Die Stammfunktion muss so ermittelt werden, dass ihre Ableitung der ursprünglichen Funktion entspricht. Daher lassen sich die Regeln zum ,,Aufleiten“ an Hand derer zum Ableiten finden.

Für die Ableitung der Funktion $F\left( x \right) = x^{a}$ gilt:

f (x) = a \cdot x^{a - 1}

$f\left( x \right) = a \cdot x^{a - 1}$

Hieraus folgt umgekehrt, wenn $f\left( x \right) = x^{a}$ ist, dass

F (x) = \frac{1}{a + 1} \cdot x^{a + 1}

$F\left( x \right) = \frac{1}{a + 1} \cdot x^{a + 1}$

Bei Stammfunktion zu Summen von Funktionen, wird für jeden Summanden die Stammfunktion gesucht.

Für Lineare Verkettungen ( $F\left( h\left( x \right) \right)$ ) gilt bei der Ableitung:

f (h (x)) \cdot h ´ (x)

$f\left( h\left( x \right) \right) \cdot h´(x)$

Dementsprechend gilt bei der ,,Aufleitung“ von $f(h\left( x \right))$ :

F (h (x)) \cdot \frac{1}{h ´ (x)}

$F(h\left( x \right)) \cdot \frac{1}{h´(x)}$

Also bei dem Beispiel $f\left( x \right) = {(2x + 3)}^{2}$ :

\frac{1}{3} {(2 x + 3)}^{3} \cdot \frac{1}{2} = \frac{1}{6} {(2 x + 3)}^{3}

$\frac{1}{3}{(2x + 3)}^{3} \cdot \frac{1}{2} = \frac{1}{6}{(2x + 3)}^{3}$

Da alleinstehende Zahlen bei der Ableitung wegfallen, gibt es unendlich viele ,,Aufleitungen“ (+c). Durch die Subtraktion in $F\left( b \right) - F(a)$ fällt das +c allerdings weg.

Hinweis: Die ,,Aufleitung“ von $x^{- 1}$ ist $ln(x)$ .

Integration durch Substitution

\int_{a}^{b} f (g (x)) \times g ‘ (x) d x = \int_{g (a)}^{g (b)} f (z) dz

$\int_{a}^{b}{f\left( g(x) \right) \times g`(x)dx} = \int_{g(a)}^{g(b)}{f\left( z \right)\text{dz}}$

Um die erste Form zu erhalten, muss teilweise ergänzt werden. Die einfachste Methode ist, Brüche falls vorhanden umzuschreiben und dann die benötigte Zahl sowie ihren Kehrwert als Multiplikation in das Integral zu ziehen und den nicht benötigten Faktor vor das Integral zu holen.

Beispiel:

\int_{0}^{2} \frac{4 x}{\sqrt{1 + {2 x}^{2}}} = \int_{0}^{2} 4 x \times {(1 + {2 x}^{2})}^{- \frac{1}{2}}

$\int_{0}^{2}{\frac{4x}{\sqrt{1 + {2x}^{2}}} = \int_{0}^{2}{4x \times \left( 1 + {2x}^{2} \right)^{- \frac{1}{2}}}}$

f (x) = x^{- \frac{1}{2}}

$f\left( x \right) = x^{- \frac{1}{2}}$

g (x) = 1 + {2 x}^{2}

$g\left( x \right) = 1 + {2x}^{2}$

g (0) = 1

$g\left( 0 \right) = 1$

g (2) = 9

$g\left( 2 \right) = 9$

\int_{0}^{2} 4 x \times {(1 + {2 x}^{2})}^{- \frac{1}{2}} d x = \int_{1}^{9} z^{- \frac{1}{2}} dz

$\int_{0}^{2}{4x \times \left( 1 + {2x}^{2} \right)^{- \frac{1}{2}}}dx = \int_{1}^{9}z^{- \frac{1}{2}}\text{dz}$

f (z) = z^{- \frac{1}{2}}

$f\left( z \right) = z^{- \frac{1}{2}}$

F (z) = 2 z^{\frac{1}{2}}

$F\left( z \right) = 2z^{\frac{1}{2}}$

\int_{1}^{9} z^{- \frac{1}{2}} d z = 2 \times 3 - 2 \times 1 = 4

$\int_{1}^{9}z^{- \frac{1}{2}}dz = 2 \times 3 - 2 \times 1 = 4$

Herleitung

Aus der Form $\int_{a}^{b}{f\left( g(x) \right) \times g`(x)dx}$ wird wegen der Kettenregel ersichtlich, dass $F(g\left( x \right))$ die Stammfunktion dieser Funktion ist. Denn nach der Kettenregel ist die Ableitung von $F(g\left( x \right))$ $f\left( g(x) \right) \times g`(x)$ . Daraus ergibt sich:

\int_{a}^{b} f (g (x)) \times g ‘ (x) d x = [F (g (x))] \begin{matrix} b \\ a \end{matrix} = \int_{g (a)}^{g (b)} f (z) dz

$\int_{a}^{b}{f\left( g(x) \right) \times g`(x)dx} = \left\lbrack F(g\left( x \right)) \right\rbrack\begin{matrix} b \\ a \\ \end{matrix} = \int_{g(a)}^{g(b)}{f\left( z \right)\text{dz}}$

Partielle Integration

Für verkettete Funktionen $f = g \times h\$ wird die Stammfunktion bestimmt, indem versucht wird, die Produktregel umzukehren. Es ergibt sich folgende Formel:

\int_{a}^{b} (u ´ (x) \times v (x)) d x = [u (x) \times v (x)] \begin{matrix} b \\ a \end{matrix} - \int_{a}^{b} (u (x) \times v ´ (x)) dx

$\int_{a}^{b}{\left( u´(x) \times v(x) \right)dx = \left\lbrack u(x) \times v(x) \right\rbrack\begin{matrix} b \\ a \\ \end{matrix} - \int_{a}^{b}{\left( u\left( x \right) \times v´(x) \right)\text{dx}}}$

Hierbei werden g und h u´ und v so zugeordnet, dass es nicht zu einem endlosen Vorgang (sondern einem möglichst kurzen) kommt. Die Ableitung von v sollte nicht v ergeben, nicht negativ sein und die Potenz der Variable sollte so niedrig wie möglich über 0 liegen. Teilweise können mehrere Schritte erforderlich sein.

Herleitung / Eselsbrücke

[u (x) \times v (x)] \begin{matrix} b \\ a \end{matrix} = \int_{a}^{b} (u ´ (x) \times v (x)) d x + \int_{a}^{b} (u (x) \times v ´ (x)) dx

$\left\lbrack u(x) \times v(x) \right\rbrack\begin{matrix} b \\ a \\ \end{matrix} = \int_{a}^{b}{\left( u´(x) \times v(x) \right)dx + \int_{a}^{b}{\left( u\left( x \right) \times v´(x) \right)\text{dx}}}$

\int_{a}^{b} (u ´ (x) \times v (x)) d x = [u (x) \times v (x)] \begin{matrix} b \\ a \end{matrix} - \int_{a}^{b} (u (x) \times v ´ (x)) dx

Steht alles in der Form: $\left\lbrack \text{what} \right\rbrack\begin{matrix} b \\ a \\ \end{matrix} - \left\lbrack \text{ever} \right\rbrack\begin{matrix} b \\ a \\ \end{matrix}$ so wurde hiermit die Stammfunktion $F = what - ever$ gefunden.

Beispiel:

f (x) = x \times s i n (x)

$f\left( x \right) = x \times sin(x)$

u ‘ = s i n (x)

$u` = sin(x)$

u = - c o s (x)

$u = - cos(x)$

v = x

$v = x$

v ‘ = 1

$v` = 1$

\int_{a}^{b} (s i n (x) \times x) d x = [- c o s (x) \times x] \begin{matrix} b \\ a \end{matrix} - \int_{a}^{b} (- c o s (x)) dx = [- c o s (x) \times x] \begin{matrix} b \\ a \end{matrix} - [- s i n (x)] \begin{matrix} b \\ a \end{matrix}

$\int_{a}^{b}{\left( sin(x) \times x \right)dx = \left\lbrack - cos(x) \times x \right\rbrack\begin{matrix} b \\ a \\ \end{matrix} - \int_{a}^{b}{\left( - cos(x) \right)\text{dx}}} = \left\lbrack - cos(x) \times x \right\rbrack\begin{matrix} b \\ a \\ \end{matrix} - \left\lbrack - sin(x) \right\rbrack\begin{matrix} b \\ a \\ \end{matrix}$

F (x) = - \cos (x) \times x + s i n (x)

$F\left( x \right) = - \cos\left( x \right) \times x + sin(x)$

Integral und Flächeninhalt

Unter der x-Achse liegende Flächen

Liegt die Fläche unter der x-Achse, so ist das Integral negativ (in diesem Bereich nimmt der Wert der Stammfunktion ab). Da eine Fläche nicht negativ sein kann, wird der Betrag des Integrals verwendet.

undefined

A = | \int_{a}^{b} ({- x}^{2}) d x |

$A = \left| \int_{a}^{b}{({- x}^{2}})dx \right|$

Liegt ein Teil der Fläche über und ein Teil unter der x-Achse, so müssen beide Teilflächen einzeln berechnet und summiert werden.

Zwischen zwei Graphen liegende Fläche

Falls die Fläche die x-Achse überschreitet, müssen beide Graphen so entlang der y-Achse verschoben werden (+/-d), sodass dies nicht mehr der Fall ist.
Die Fläche wird berechnet, indem von der Fläche des Graphen mit der größeren Fläche die des Graphen mit der kleineren Fläche abgezogen wird.

A = \int_{a}^{b} f (x) d x - \int_{a}^{b} g (x) d x = \int_{a}^{b} f (x) - g (x)) d x

$A = \int_{a}^{b}{f\left( x \right)dx -}\int_{a}^{b}{g\left( x \right)dx = \int_{a}^{b}{f\left( x \right) - g(x))dx}}$

Bei Flächen unterhalb der x-Achse muss der Betrag verwendet werden.

Zu beachten ist, dass durch das Integral der orientierte Flächeninhalt zwischen Graph und Achse berechnet wird.

Integral und Rauminhalt

Wird ein Graph um die x-Achse rotiert, so erhält man einen Rotationskörper. Das Volumen des entstehenden Körpers kann (Analog zu den Rechtecken bei der Fläche) durch Zylinder berechnet werden.

$V = \pi{(f(x_{1}))}^{2} \times \mathrm{\Delta}x + \pi{(f(x_{2}))}^{2} \times \mathrm{\Delta}x\ldots. = \int_{a}^{b}{\pi \times {f(x)}^{2}\text{dx}}$ = $\text{π}\int_{a}^{b}{{f(x)}^{2}\text{dx}}$

Rotationskörper durch die Rotation einer Fläche zwischen zwei Funktionen

Wird eine Fläche zwischen zwei Funktionen rotiert, so muss aufgrund der Rolle des Umfangs (weiter außen liegende Fläche → mehr Volumen bei Rotation) erst das Volumen des Rotationskörpers der höher liegenden Funktion berechnet werden, von welchem dann das Volumen des Rotationskörpers der anderen Funktion abgezogen wird.

V = π \int_{a}^{b} {f (x)}^{2} dx - π \int_{a}^{b} {g (x)}^{2} d x = π \int_{a}^{b} ({f (x)}^{2} - {g (x)}^{2}) d x

$V = \pi\int_{a}^{b}{{f(x)}^{2}\text{dx}} - \pi\int_{a}^{b}{{g(x)}^{2}dx = \pi\int_{a}^{b}{({f(x)}^{2} - {g\left( x \right)}^{2})dx}}$

Auch eventuell interessant: Zusammenfassung zur analytischen Geometrie

Empfehlungen

Analytische Geometrie - Themen

PowerPoint Presentation: Cryptography – Is our privacy in jeopardy?

Castellio - gemeinfreie Werke frei verfügbar

Stefan Zweigs Werke

Sie möchten mir einen Kaffee spendieren?

Anmerkungen oder sonstige Ideen und Vorschläge können Sie gern per Mail an info@lernzettel.org bzw. fehler@lernzettel.org senden.