Analytische Geometrie Zusammenfassung Abitur

Analytische Geometrie - Themen

1. Vektoren

   1. Skalarprodukt

   2. Kreuzprodukt

   3. Länge

   4. Einheitsvektor

2. Gauß-Verfahren

3. Geraden

   1. Parameterform

   2. Normalenform

   3. Koordinatenform

   4. Punktprobe

4. Lage zweier Geraden zueinander

5. Ebenen

   1. Parameterform

      1. Punktprobe

      2. Aufstellen aus

         1. Drei Punkten

         2. Einer Gerade und einem Punkt

      3. Umformen aus anderen Formen

   2.  Normalenform

      1. Umformen aus anderen Formen

   3.  Koordinatenform

      1. Umformen aus anderen Formen

      2. Spurpunkte

      3. Spurgeraden

6. Lagebeziehungen Ebene zu Ebene

7. Lagebeziehungen Gerade zu Ebene

8. Abstandsbestimmung Punkt zu Ebene

   1. Durch Lotgerade

   2. Hessesche Normalenform

9. Abstand Punkt zu Gerade

10. Abstand Gerade zu Gerade

11. Schnittwinkel

12. Kreise und Kugeln

    1. Gleichungen

    2. Lagebeziehungen Kugel zu Ebene

Beschriftung des Koordinatensystems und eines Vierecks

Koordinatensystem

Viereck

Skalarprodukt

$$\overrightarrow{a} \cdot \overrightarrow{b} = \left| \overrightarrow{a} \right| \cdot \left| \overrightarrow{b} \right| \cdot \cos\left( \alpha \right) = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}$$

Zwei Vektoren stehen senkrecht zueinander (orthogonal), wenn ihr
Skalarprodukt null ergibt, da gilt:
$\cos\left( 90{^\circ} \right) = 0$.

Kreuzprodukt

Das Kreuzprodukt $\overrightarrow{a} \times \overrightarrow{b}$ lässt sich nach folgendem Schema berechnen. Der resultierende Vektor ist senkrecht zu den beiden ursprünglichen.

$$\overrightarrow{a} \times \overrightarrow{b} = \begin{pmatrix} a_{2}b_{3} - a_{3}b_{2} \\ a_{3}b_{1} - a_{1}b_{3} \\ a_{1}b_{2} - a_{2}b_{1} \\ \end{pmatrix}$$

Geometrische Bedeutung

Länge von Vektoren

Die Länge ist die Wurzel der Summe aller quadrierten Komponenten.

$$\left| \overrightarrow{a} \right| = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}}$$

Einheitsvektor

Vektor mit der gleichen Richtung des ursprünglichen Vektors und der
Länge eins.

$$\overrightarrow{a_{\text{einheits}}} = \frac{\overrightarrow{a}}{\left| \overrightarrow{a} \right|}$$

Gauß-Verfahren

Der Gauß-Algorithmus wird dazu verwendet, lineare Gleichungssysteme zu lösen.

Dies wird anhand eines Beispiels erklärt:

Es sind folgende Gleichungen gegeben:

$$x_{1} - x_{2} + 2x_{3} = 0$$

$$- 2x_{1} + x_{2} - 6x_{3} = 0$$

$$x_{1} - 2x_{3} = 3$$

Nun werden die Gleichungen ohne die Variablen notiert:

$$\left| \begin{matrix} 1 & - 1 & 2 \\ - 2 & 1 & - 6 \\ 1 & 0 & - 2 \\ \end{matrix} \right|\begin{matrix} 0 \\ 0 \\ 3 \\ \end{matrix}$$

Ziel ist eine stufenförmige Anordnung der Nullen nach diesem oder einem ähnlichen Muster:

$$\left| \begin{matrix} x & x & x \\ 0 & x & x \\ 0 & 0 & x \\ \end{matrix} \right|\begin{matrix} x \\ x \\ x \\ \end{matrix}$$

Hierdurch kann dann von unten aufgelöst werden. Um dies zu erreichen, können mehrere Operationen angewendet werden:

1. Zeilen vertauschen

2. Eine Zeile durch die Summe von ihr und einer anderen Zeile ersetzen

3. Zeilen mit einer Zahl (ungleich 0) multiplizieren 

Für das Beispiel ergibt sich:

• 2. Zeile durch die Summe der ersten und zweiten Zeile ersetzen

• 3. Zeile durch Summe der 3. und 2. Zeile ersetzen

$$\left| \begin{matrix} 1 & - 1 & 2 \\ - 2 & 1 & - 6 \\ 1 & 0 & - 2 \\ \end{matrix} \right|\begin{matrix} 0 \\ 0 \\ 3 \\ \end{matrix}\ \rightarrow \ \left| \begin{matrix} 1 & - 1 & 2 \\ - 1 & 0 & - 4 \\ 1 & 0 & - 2 \\ \end{matrix} \right|\begin{matrix} 0 \\ 0 \\ 3 \\ \end{matrix} \rightarrow \ \left| \begin{matrix} 1 & - 1 & 2 \\ - 1 & 0 & - 4 \\ 0 & 0 & - 6 \\ \end{matrix} \right|\begin{matrix} 0 \\ 0 \\ 3 \\ \end{matrix}$$

• Auflösen der letzten Zeile

$${- 6x}_{3} = 3$$

$$x_{3} = - 0,5$$

• Auflösen der zweiten Zeile durch das Ergebnis der 3.

$${- x}_{1} - 4\left( - 0,5 \right) = 0$$

$$x_{1} = 2$$

• 1. Zeile durch die Ergebnisse der 2. und 3.

$$2 - x_{2} + 2\left( - 0,5 \right) = 0$$

$$2 - x_{2} - 1 = 0$$

$$1 - x_{2} = 0$$

$$x_{2} = 1$$

Geraden - Formen und Punktprobe

Parameterform

$$g:\overrightarrow{x} = \overrightarrow{p} + t \cdot \overrightarrow{r}$$

$$\overrightarrow{p} = Ortsvektor$$

$$\overrightarrow{r} = Richtungsvektor$$

Über diese Gleichung sind alle Punkte auf der Geraden definiert, sie sind vom Ortsvektor aus über den Richtungsvektor zu erreichen.

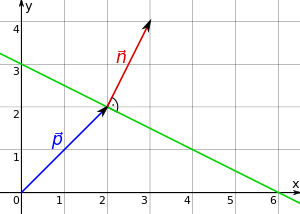
Normalenform

Eine Gerade im zweidimensionalen Raum kann durch die Normalenform bestimmt werden. Sie kann durch einen Stützvektor $\overrightarrow{p}$, welcher der Ortsvektor eines auf der Gerade liegenden Punktes ist und den Normalenvektor $\overrightarrow{n}$, welcher mit der Gerade einen rechten Winkel bildet, dargestellt werden.

Ein Punkt für dessen Ortsvektor $\left( \overrightarrow{x} - \overrightarrow{p} \right) \cdot \overrightarrow{n} = 0$ gilt, liegt auf der Gerade.

Berechnung aus der Parameterform

Der Stützvektor bleibt gleich. Für den Normalenvektor werden die Komponenten des Richtungsvektors und bei einer Komponente das Vorzeichen vertauscht.

Lizenz

Koordinatenform

Im zweidimensionalen Raum kann eine Gerade auch durch die Koordinatenform beziehungsweise als lineare Gleichung durch drei reelle Zahlen beschrieben werden.

$$ax + by = c$$

Diese Form entsteht durch ausmultiplizieren der Normalenform.

Punktprobe

Punkt mit Geradengleichung gleichsetzen, t berechnen (muss für jede ,,Zeile“ gleich sein).

[i] Quartl, Line equation qtl3, CC BY-SA 3.0

Lagebeziehungen zweier Geraden zueinander

1. Parallel

   1. Richtungsvektoren sind Vielfache

2. Identisch

   1. Richtungsvektoren sind Vielfache & Geraden teilen alle Punkte

3. Schnittpunkt

   1. Geradengleichungen gleichsetzen und auflösen

4. Windschief

   1. Die Geraden verlaufen weder parallel noch schneiden sie sich, beim Gleichsetzen der Geradengleichung gibt es keine Lösung und die Richtungsvektoren sind keine Vielfache → siehe Abstandsbestimmung bei Geraden

Ebenen - Gleichungsformen, Umwandlungen, Spurgeraden und Punke

Die Ebene ist ein unbegrenzt ausgedehntes zweidimensionales Objekt.

Parametergleichung

Die Ebene kann durch die Parametergleichung ausgedrückt werden, welche diese Form besitzt:

$$E:\overrightarrow{x} = \overrightarrow{p} + r \cdot \overrightarrow{u} + s \cdot \overrightarrow{v}$$

$$\overrightarrow{p} = Stützvektor$$

$$\overrightarrow{u},\ \overrightarrow{v} = Spannvektoren$$

Erstellen aus drei Punkten

Einer der Punkte wird als Stützvektor genommen, die Spannvektoren sind die Vektoren, welche vom Stützvektor aus zu jeweils einem anderen Punkten führen.

Erstellen aus einer Gerade und einem Punkt

Der Punkt darf nicht auf der Geraden liegen, der Stützvektor und der Richtungsvektor als ein Spannvektor werden übernommen, der zweite Spannvektor ist der vom Stützvektor zum Punkt führende Vektor.

Punktprobe

Gleichsetzten des Punktes mit der Ebenengleichung und auflösen.

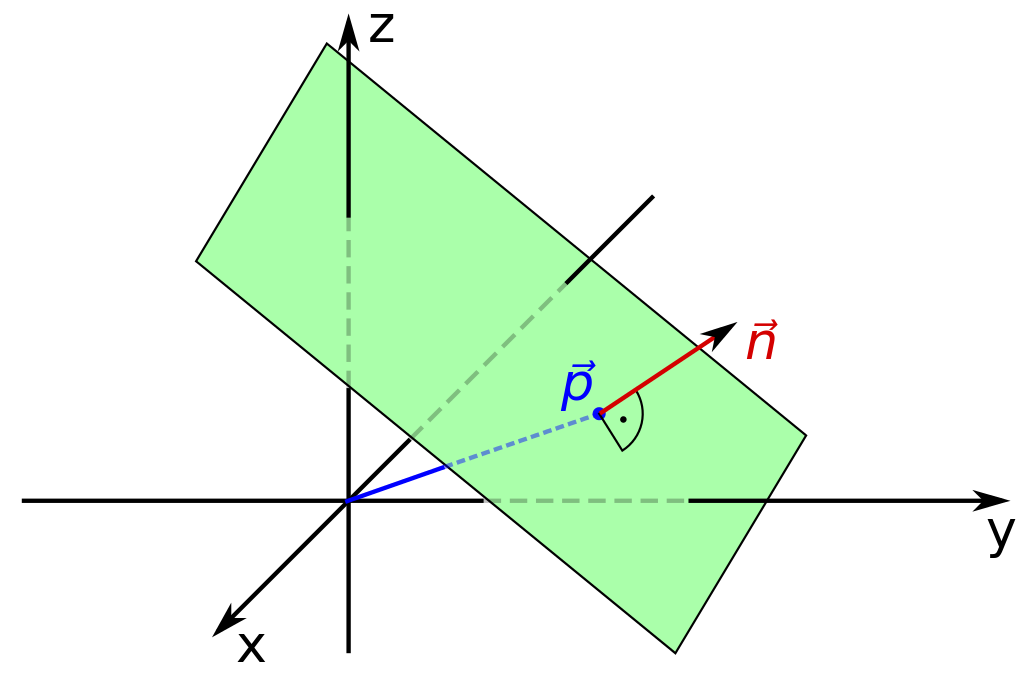
Normalenform

$$\left( \overrightarrow{x} - \overrightarrow{p} \right) \cdot \overrightarrow{n} = 0$$

$$\overrightarrow{p} = Stützvektor\ (Punkt\ auf\ der\ Ebene)$$

$$\overrightarrow{n} = Senkrecht\ zur\ Ebene\ stehender\ Normalenvektor$$

$$\overrightarrow{x} = Punkt\ auf\ der\ Ebene,\ falls\ die\ Bedingung\ erfüllt\ ist$$

Lizenzhinweis: Quartl, Plane equation qtl3, CC BY-SA 3.0

Berechnung aus der Parameterform

$$\overrightarrow{p} = \overrightarrow{p}$$

$$\overrightarrow{n} = \overrightarrow{u} \times \overrightarrow{v}$$

Koordinatenform

Die Ebene kann durch vier reelle Zahlen beschrieben werden.

$$ax_{1} + bx_{2} + cx_{3} = d$$

Diese Form ist die ausmultiplizierte Normalenform.

$$a = n_{1}$$

$$b = n_{2}$$

$$c = n_{3}$$

$$d = \overrightarrow{p} \cdot \overrightarrow{n}$$

Spurpunkte

Die Spurpunkte sind solche Punkte, an welchen die Ebene eine Achse schneidet. Hier ist der Wert aller Koordinaten, außer der der Achse, welche geschnitten wird, gleich 0. Für die -Achse setzt man so  und  gleich 0 und berechnet den Wert für . So ergeben sich maximal drei Spurpunkte. Fehlt ein Spurpunkt, so herrscht Parallelität zu dieser Achse.

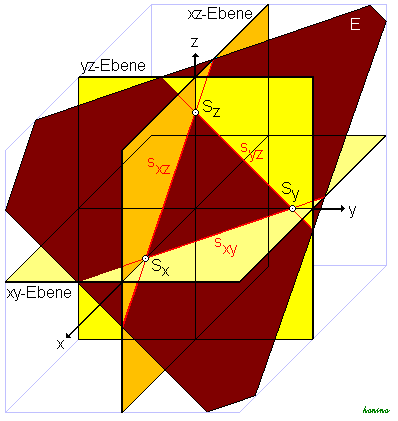
Spurgeraden

Die Spurpunkte werden von den Spurgeraden verbunden. Diese sind die Schnittgeraden einer Ebene mit einer Grundebene des räumlichen Koordinatensystems.

Lizenzhinweis: Honina, Spurgeraden und Punkte, CC BY-SA 3.0

Von der Koordinatenform zur Parameterform

Aus den Spurpunkten kann die Parameterform erstellt werden.

Von der Koordinatenform zur Normalenform

Über a, b und c kann der Normalenvektor bestimmt werden. Zur Bestimmung eines Stützvektors werden zwei Komponente des -Vektors beliebig festgelegt und die dritte durch Einsetzten bestimmt.

Gegenseitige Lage von Ebenen

Für zwei Ebenen gibt es drei mögliche Lagebeziehungen:

1. Sie sind identisch

2. Sie sind parallel

3. Sie schneiden sich in einer Schnittgerade

Um festzustellen, welche Lagebeziehung vorliegt, gibt es mehrere Verfahren.

Beide Ebenen liegen in der Koordinaten- oder Normalenform vor

1. Sind die Normalenvektoren parallel, sind die Ebenen entweder parallel oder identisch.

Gegeben sind $E:2x_{1} + 3x_{2} - x_{3} = 5$ und $F:4x_{1} + 6x_{2} - 2x_{3} = 3$. Folglich sind die Normalenvektoren $\overrightarrow{\text{NE}} = \begin{pmatrix} 2 \\ 3 \\ - 1 \\ \end{pmatrix}$ und $\overrightarrow{\text{NF}} = \begin{pmatrix} 4 \\ 6 \\ - 2 \\ \end{pmatrix}$. Die Normalenvektoren sind vielfach voneinander, sie sind parallel.

2. Um zu prüfen, ob die Ebenen identisch sind, wird ein beliebiger Punkt aus der einen in die andere Ebene eingesetzt (identische Ebenen teilen alle Punkte). Um einen beliebigen Punkt zu erhalten, werden in der Koordinatenform x1 und x2 beliebig gesetzt und x3 berechnet.

$$2x_{1} + 3x_{2} - x_{3} = 5$$

$$x_{1} = 0;\ x_{2} = 0;x_{3} = - 5$$

Eingesetzt in F: $10 \neq 3$. Die Ebenen sind parallel und nicht identisch.

3. Sind die Normalenvektoren nicht parallel, gibt es eine Schnittgerade. Diese kann wie folgt berechnet werden.

a. Stufensystem aufstellen

$$2x_{1} + 3x_{2} - x_{3} = 5\ $$

$$- 5x_{1} + 10x_{2} - x_{3} = 5$$

Ich ersetze die 2. Zeile durch die Summe von ihr und der ersten Zeile Mal -1.

$$2x_{1} + 3x_{2} - x_{3} = 5\ $$

$$- 7x_{1} + 7x_{2} = 0$$

b. Eine Variable, welche in beiden Gleichungen vorkommt, gleich t setzen und zu den Variablen auflösen

$$x_{1} = t$$

$$x_{2} = t$$

$${- x}_{3} = 5 - 2t - 3t$$

$${- x}_{3} = 5 - 5t$$

$$x_{3} = - 5 + 5t$$

c. In Geradengleichung umstellen

$$g:\ \overrightarrow{x} = \begin{pmatrix} 0 \\ 0 \\ - 5 \\ \end{pmatrix} + t\begin{pmatrix} 1 \\ 1 \\ 5 \\ \end{pmatrix}$$

Eine Ebene liegt in der Parametergleichung, die andere in der Koordinatengleichung vor

Gegeben sind $E:2x_{1} + 3x_{2} - x_{3} = 5\ $ und $F:\overrightarrow{x} = \begin{pmatrix} 1 \\ 1 \\ 5 \\ \end{pmatrix} + r\begin{pmatrix} 2 \\ 1 \\ 0 \\ \end{pmatrix} + s\begin{pmatrix} - 1 \\ 0 \\ 5 \\ \end{pmatrix}$.

Jede der Zeilen in der Parametergleichung steht für eine Komponente des Vektors x. Die erste Zeile steht für x1 usw.. 

1. Die Zeilen der Parametergleichung werden in die Koordinatengleichung eingesetzt

$$2\left( 1 + 2r - s \right) + 3\left( 1 + r \right) - 5 - 5s = 5\ $$

Beim Auflösen können drei Möglichkeiten auftreten:

a. Eine wahre Aussage ergibt sich (z. B. 4=4) → identisch

b. Eine falsche Aussage ergibt sich (z. B. 1=5) → parallel

c. r &/ s bleiben bestehen → Schnittgerade

$$2 + 4r - 2s + 3 + 3r - 5 - 5s = 5$$

$$7r - 7s = 5$$

$$7r = 5 + 7s$$

$$r = \frac{5}{7} + s$$

Fall 3. ist hier eingetreten.

2. Das Ergebnis wird beim 3. Fall in die Parametergleichung eingesetzt, um die Gleichung der Schnittgerade herauszufinden.

$$G:\overrightarrow{x} = \begin{pmatrix} 1 \\ 1 \\ 5 \\ \end{pmatrix} + \left( \frac{5}{7} + s \right)\begin{pmatrix} 2 \\ 1 \\ 0 \\ \end{pmatrix} + s\begin{pmatrix} - 1 \\ 0 \\ 5 \\ \end{pmatrix} = \begin{pmatrix} 1 + \frac{10}{7} \\ 1 + \frac{5}{7} \\ 5 \\ \end{pmatrix} + s\begin{pmatrix} 1 \\ 1 \\ 5 \\ \end{pmatrix}$$

Beide Ebenen liegen in Parameterform vor

Zwei Ebenen in Parameterform sind gegeben. Ziel ist, für eine der beiden Ebenen einen der Vorfaktoren in Abhängigkeit des anderen auszudrücken.

$$E:\overrightarrow{x} = \begin{pmatrix} 8 \\ 0 \\ 2 \\ \end{pmatrix} + r\begin{pmatrix} - 4 \\ 1 \\ 1 \\ \end{pmatrix} + s\begin{pmatrix} 5 \\ 0 \\ - 1 \\ \end{pmatrix}$$

$$F:\overrightarrow{x} = \begin{pmatrix} 1 \\ 0 \\ 1 \\ \end{pmatrix} + t\begin{pmatrix} - 3 \\ 0 \\ 1 \\ \end{pmatrix} + u\begin{pmatrix} 1 \\ 4 \\ 1 \\ \end{pmatrix}$$

Für das Beispiel bedeutet dies, dass eine Relation zwischen r und s oder u und t gesucht ist.

1. Ein lineares Gleichungssystem wird hierzu aufgestellt, wobei darauf zu achten ist, nicht die gleichen Symbole für den Vorfaktor der Spannvektoren zu nehmen (nicht zweimal r/s)

a. Die Ebenen in Parameterform werden gleichgesetzt

$$\begin{pmatrix} 8 \\ 0 \\ 2 \\ \end{pmatrix} + r\begin{pmatrix} - 4 \\ 1 \\ 1 \\ \end{pmatrix} + s\begin{pmatrix} 5 \\ 0 \\ - 1 \\ \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \\ \end{pmatrix} + t\begin{pmatrix} - 3 \\ 0 \\ 1 \\ \end{pmatrix} + u\begin{pmatrix} 1 \\ 4 \\ 1 \\ \end{pmatrix}$$

b. Die Gleichungen werden so umgestellt, dass die Vektoren ohne Variable auf der einen und die mit auf der anderen Seite stehen

$$\begin{pmatrix} 7 \\ 0 \\ 1 \\ \end{pmatrix} = t\begin{pmatrix} - 3 \\ 0 \\ 1 \\ \end{pmatrix} + u\begin{pmatrix} 1 \\ 4 \\ 1 \\ \end{pmatrix} - r\begin{pmatrix} - 4 \\ 1 \\ 1 \\ \end{pmatrix} - s\begin{pmatrix} 5 \\ 0 \\ - 1 \\ \end{pmatrix}$$

c. Ein LGS nach dem Gauß-Verfahren wird aufgestellt und in eine Stufenform gelöst

$$\left| \begin{matrix} t & u & r & s \\ - 3 & 1 & 4 & - 5 \\ 0 & 4 & - 1 & 0 \\ 1 & 1 & - 1 & 1 \\ \end{matrix} \right|\begin{matrix} = \\ 7 \\ 0 \\ 1 \\ \end{matrix} \rightarrow \left| \begin{matrix} t & u & r & s \\ - 3 & 1 & 4 & - 5 \\ 0 & 4 & - 1 & 0 \\ 0 & 0 & 2 & - 2 \\ \end{matrix} \right|\begin{matrix} = \\ 7 \\ 0 \\ 10 \\ \end{matrix}\ $$

d. Die letzte Zeile wird herausgeschrieben

$$2r - 2s = 10$$

$$r = 5 + s$$

In der letzten Zeile können drei Fälle auftreten

1. Eine wahre Aussage ergibt sich ((alle Variablen fallen weg)0=0) → identisch

2. Es gibt keine Lösung ((alle Variablen fallen weg)→ 0=7) → parallel

3. Zwei Variablen lassen sich in Abhängigkeit zueinander stellen → Schnittgerade

2. Tritt der dritte Fall ein, kann eine Schnittgerade berechnet werden. Hierfür wird das Ergebnis so eingesetzt, dass in der gewählten vorherigen Ebenengleichung nur eine Variable übrigbleibt.

$$G:\overrightarrow{x} = \begin{pmatrix} 8 \\ 0 \\ 2 \\ \end{pmatrix} + \left( 5 + s \right)\begin{pmatrix} - 4 \\ 1 \\ 1 \\ \end{pmatrix} + s\begin{pmatrix} 5 \\ 0 \\ - 1 \\ \end{pmatrix} = \begin{pmatrix} - 12 \\ 5 \\ 7 \\ \end{pmatrix} + s\begin{pmatrix} 1 \\ 1 \\ 0 \\ \end{pmatrix}$$

Gegenseitige Lage von Geraden und Ebenen

Ebenen und Geraden können auf drei verschiedene Weisen zueinander liegen:

1. Die Gerade verläuft in der Ebene

2. Die Gerade schneidet die Ebene

3. Die Gerade liegt parallel zur Ebene

Welcher Fall vorliegt kann durch verschiedene Verfahren bestimmt werden.

Bestimmung der Lage durch ein lineares Gleichungssystem

Für diese Methode muss die Ebene in der Koordinaten- und die Geraden in der Parameterform vorliegen. Ist dies nicht der Fall müssen die Formen durch Umwandlungen erreicht werden.

Das Verfahren wird an Hand eines Beispiels erklärt:

Gleichung der Ebene in Koordinatenform: $E:2x_{1} + 3x_{2} - x_{3} = 4$

Gleichung der Gerade in Parameterform: $g:\overrightarrow{x} = \begin{pmatrix} 3 \\ 2 \\ 1 \\ \end{pmatrix} + t\begin{pmatrix} 2 \\ 1 \\ 0 \\ \end{pmatrix}$

1. Die Geradengleichung wird in die einzelnen Komponenten geteilt

$$x_{1} = 3 + 2t$$

$$x_{2} = 2 + t$$

$$x_{3} = 1$$

2. Die Komponenten werden in die Koordinatenform der Ebene eingesetzt

$$2(3 + 2t) + 3(2 + t) - 1 = 4$$

3. Es wird nach t aufgelöst

$$6 + 4t + 6 + 3t - 1 = 4$$

$$11 + 7t = 4$$

$$7t = - 7$$

$$t = - 1$$

Hier können drei Möglichkeiten auftreten:

1. t kann bestimmt werden → Schnittpunkt

2. eine wahre Aussage ist das Ergebnis (z. B. 4=4) → Alle Punkte der Gerade liegen in der Ebene → Die Gerade verläuft in der Ebene

3. es gibt keine Lösung (z.B. 0=4) → die Gerade verläuft parallel zur Ebene

4. Gibt es einen Schnittpunkt wird dieser durch das Einsetzen des Wertes für t in die Geradengleichung bestimmt

$$t = - 1$$

$$S = \begin{pmatrix} 3 \\ 2 \\ 1 \\ \end{pmatrix} - \begin{pmatrix} 2 \\ 1 \\ 0 \\ \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \\ \end{pmatrix}$$

Bestimmung der Lage durch Untersuchung von Vektoren

Gegebene Formen

$$E:2x_{1} + 3x_{2} - x_{3} = 4$$

$$g:\overrightarrow{x} = \begin{pmatrix} 3 \\ 2 \\ 1 \\ \end{pmatrix} + t\begin{pmatrix} 2 \\ 1 \\ 0 \\ \end{pmatrix}$$

1. Schnittpunkt / nicht

Ob es einen Schnittpunkt / nicht gibt, kann über den Normalenvektor der Ebene und den Richtungsvektor der Gerade bestimmt werden. Der Normalenvektor steht senkrecht zur Ebene. Steht der Richtungsvektor der Gerade orthogonal zum Normalenvektor, verläuft die Gerade parallel zur oder in der Ebene. Ist dies nicht der Fall gibt es einen Schnittpunkt.

a. Normalenvektor aufstellen

$$E:2x_{1} + 3x_{2} - x_{3} = 4$$

$$\overset{⃑}{n} = \begin{pmatrix} 2 \\ 3 \\ - 1 \\ \end{pmatrix}$$

b. Über das Skalarprodukt auf Orthogonalität prüfen

$$\begin{pmatrix} 2 \\ 3 \\ - 1 \\ \end{pmatrix} \times \begin{pmatrix} 2 \\ 1 \\ 0 \\ \end{pmatrix} = 4 + 3 = 7 \neq 0$$

Die Vektoren sind nicht Orthogonal, es gibt einen Schnittpunkt.

c. Bei Orthogonalität einen beliebigen Punkt der Gerade (z. B. Ortsvektor) in die Koordinatenform der Ebene einsetzen. Befindet sich dieser in der Ebene, liegt die Gerade in der Ebene, wenn nicht verläuft die Gerade parallel.

Abstandsbestimmung Punkt zu Ebene

Lotgerade

Der Normalenvektor einer Ebene steht senkrecht zu ihr. Der gesuchte kürzeste Abstand zwischen einem Punkt und einer Ebene wird durch eine senkrecht auf der Ebene stehenden Gerade zum Punkt erreicht. Um den Abstand zu bestimmen geht man wie folgt vor:

1. Eine Geradengleichung mit dem Punkt als Ortsvektor und dem Normalenvektor der Gerade als Richtungsvektor aufstellen

$$g:\overrightarrow{x} = \overrightarrow{p_{\text{punkt}}} + t \times \overrightarrow{n_{\text{Ebene}}}$$

2. Den Schnittpunkt der Gerade mit der Ebene bestimmen (siehe Merkzettel)

3. Den Vektor, welcher vom gegebenen Punkt zum Schnittpunkt führt bestimmen

4. Die Länge dieses Vektors über den Satz des Pythagoras berechnen

Hessesche Normalenform

Um von der Normalenform auf die Hessesche Normalenform zu kommen, wird der Normalenvektor durch dessen Einheitsvektor vertauscht.

Normalenform

$$\left\lbrack \overrightarrow{x} - \overrightarrow{p} \right\rbrack \circ \overrightarrow{n} = 0$$

$$\overrightarrow{x} = eingesetzter\ Punkt$$

$$\overrightarrow{p} = Punkt\ auf\ der\ Ebene$$

$$\overrightarrow{n} = Normalenvektor$$

Hessesche Normalenform

$$\overrightarrow{n_{\text{einheits}}} = \frac{\overrightarrow{n}}{|\overrightarrow{n}|}$$

$$\left| \overrightarrow{n} \right| = \sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}$$

$$\left\lbrack \overrightarrow{x} - \overrightarrow{p} \right\rbrack \circ \overrightarrow{n_{\text{einheits}}} = 0$$

Abstand vom Punkt zur Ebene mit der Hesseschen Normalenform

Methode 1: Einsetzen in die Hessesche Normalenform

$$|\left\lbrack \overrightarrow{x} - \overrightarrow{p} \right\rbrack \circ \overrightarrow{n_{\text{einheits}}}| = d$$

Für x wird der Punkt zu welchem der Abstand berechnet wird eingesetzt. Die Betragsstriche existieren, da die Entfernung nicht negativ sein kann.

Methode 2: Abstand, falls die Ebene in Koordinatenform vorliegt

 

$$d = \left| \frac{a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} - b}{\sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}}} \right|$$

Man setzt den Punkt in die nach 0 umgestellte Koordinatenform ein und teilt durch die Länge des Normalenvektors.

Herleitung

$\cos\left( \alpha \right) = \frac{\text{Amkathete}}{\text{Hypotenuse}} = \frac{d}{|\overrightarrow{\text{AP}}|}$

Zudem ist die geometrische Definition des Skalarprodukts:

$$\overrightarrow{a} \cdot \overrightarrow{b} = \left| \overrightarrow{a} \right| \times \left| \overrightarrow{b} \right| \times \cos\sphericalangle(\overrightarrow{a},\overrightarrow{b})$$

$$\cos\sphericalangle\left( \overrightarrow{a},\overrightarrow{b} \right) = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{\left| \overrightarrow{a} \right| \times \left| \overrightarrow{b} \right|}$$

Übertragen auf die Zeichnung bedeutet dies:

$$\cos\left( \alpha \right) = \frac{\overrightarrow{\text{AP}} \cdot \overrightarrow{n}}{|\overrightarrow{\text{AP}}| \cdot |\overrightarrow{n}|}$$

Nun werden die Gleichungen für den Cosinus gleichgesetzt:

$$\frac{d}{|\overrightarrow{\text{AP}}|} = \frac{\overrightarrow{\text{AP}} \cdot \overrightarrow{n}}{|\overrightarrow{\text{AP}}| \cdot |\overrightarrow{n}|}$$

Der Betrag von AP kann herausgekürzt werden

$$d = \frac{\overrightarrow{\text{AP}} \cdot \overrightarrow{n}}{|\overrightarrow{n}|}$$

$\overrightarrow{\text{AP}}$ ist der Vektor welcher von A zu P führt, wobei ich a durch p und P durch x ersetze:

$$d = \frac{(\overrightarrow{x} - \overrightarrow{p}) \cdot \overrightarrow{n}}{|\overrightarrow{n}|}$$

$\frac{\overrightarrow{n}}{|\overrightarrow{n}|}$ ist der Einheitsvektor des Normalenvektors, also $\overrightarrow{n_{\text{einheit}}}$

Es ergibt sich die Hessesche Normalenform, wobei zur Bestimmung des Abstandes der gegebene Punkt für x eingesetzt wird.

$$\left\lbrack \overrightarrow{x} - \overrightarrow{p} \right\rbrack \times \overrightarrow{n} = d$$

Abstand Punkt zu Gerade

1. Vom Punkt ausgehende Ebene mit Richtungsvektor der Gerade als Normalenvektor bilden

2. Schnittpunkt der Gerade mit der gebildeten Ebene bestimmen

3. Entfernung des Schnittpunktes und des Punktes bestimmen

Abstand Gerade zu Gerade

Parallele Geraden

Verlaufen die Geraden parallel, so kann ein beliebiger Punkt auf einer der Geraden gewählt werden und nach ,,Abstand Punkt zu Gerade“ der Abstand bestimmt werden.

Windschiefe Geraden

Bei windschiefen Geraden muss eine Hilfsebene von einem Punkt auf einer der Geraden aus konstruiert werden. Die Stützvektoren der Ebene sind die Richtungsvektoren der Geraden, um von der einen Gerade aus eine Ebene zu erzeugen, die parallel zur anderen Gerade liegt und somit einen festen Abstand zu dieser hat. Daraufhin wird dann einfach ein Punkt, welcher auf der parallel zur Ebene laufenden Gerade liegt, in die Hessesche Normalenform der konstruierten Ebene eingesetzt.

Aus dem Text ergibt sich folgenden für die Geraden $g:\overrightarrow{x} = \overrightarrow{p} + t \cdot \overrightarrow{r}$ und $h:\overrightarrow{x} = \overrightarrow{q} + s \cdot \overrightarrow{v}$.

$$d = \left\lbrack \overrightarrow{p} - \overrightarrow{q} \right\rbrack \circ \frac{\overrightarrow{r} \times \overrightarrow{v}}{\left| \overrightarrow{r} \times \overrightarrow{v} \right|}$$

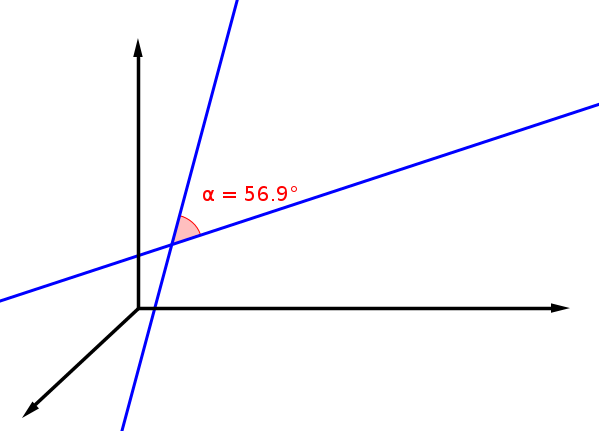
Schnittwinkel in der analytischen Geometrie

Schnittwinkel zweier Geraden

Wiederholung der Gerade-Gerade Lagebeziehungen

1. Identisch → Richtungsvektoren vielfache && erfüllte Punktprobe für alle Punkte

2. Parallel → nur Richtungsvektoren vielfache

3. Schnittpunkt → Gleichsetzen, Auflösen, Schnittpunkt ermittelbar, nicht gleich

4. Windschief → kein Schnittpunkt, nicht parallel

 

Quelle: Serlo

Hierbei sind u und v die Richtungsvektoren der Geraden.

Dies lässt sich vereinfacht aus der Definition des Skalarprodukts herleiten:

Das Skalarprodukt $\overrightarrow{u}{^\circ}\overrightarrow{v}$ ist definiert als:
$\overrightarrow{u}{^\circ}\overrightarrow{v} = \left| \overrightarrow{u} \right| \cdot \left| \overrightarrow{v} \right| \cdot cos(\alpha)$

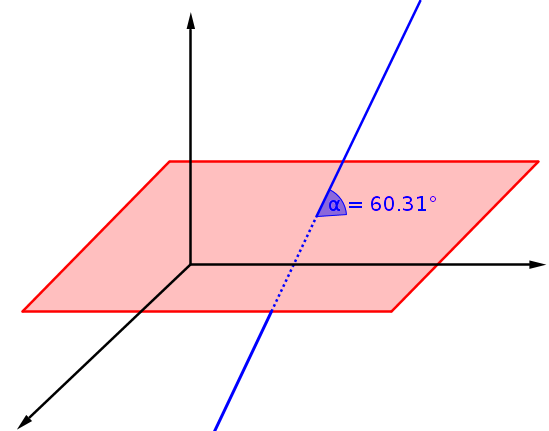
Schnittwinkel zwischen Ebene und Gerade

Schneidet eine Gerade eine Ebene in einem Schnittpunkt (siehe: Gegenseitige Lage von Geraden und Ebenen), so lässt sich auch hier der Schnittwinkel berechnen.

Quelle: Serlo

$\sin\left( \alpha \right) = \frac{\left| \overrightarrow{n}{^\circ}\overrightarrow{u} \right|}{\left| \overrightarrow{n} \right| \cdot \left| \overrightarrow{u} \right|}$

Hierbei ist n der Normalenvektor der Ebene und u der Richtungsvektor der Gerade.

Herleitung: Der Schnittwinkel zwischen der Ebene und der Gerade ist 90° minus der Schnittwinkel aus Normale der Ebene und Gerade. Daher gilt nach der obigen Herleitung:
$\cos\left( 90 - \alpha \right) = \frac{\left| \overrightarrow{n}{^\circ}\overrightarrow{u} \right|}{\left| \overrightarrow{n} \right| \cdot \left| \overrightarrow{u} \right|}$,
beziehungsweise
$\sin\left( \alpha \right) = \frac{\left| \overrightarrow{n}{^\circ}\overrightarrow{u} \right|}{\left| \overrightarrow{n} \right| \cdot \left| \overrightarrow{u} \right|}$.

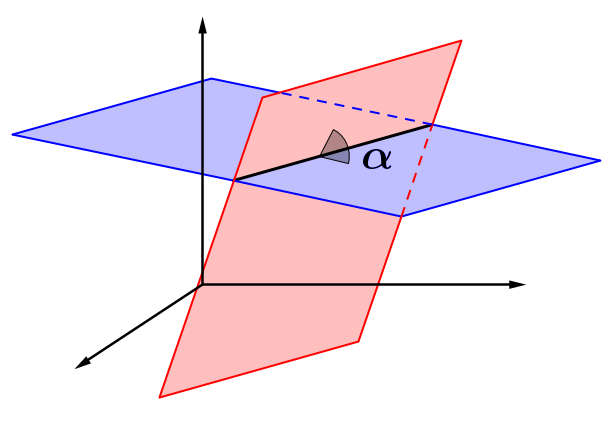
Schnittwinkel zweier Ebenen

Quelle: Serlo

Ebenen können sich in einer Schnittgeraden schneiden. Da die Normalen einen festen Winkel zu ihrer Ebene besitzen (90°), entspricht ihr Schnittwinkel (der der Normalen der Ebenen) dem der Ebenen. Somit gilt:
$\cos\left( \alpha \right) = \frac{\left| \overrightarrow{n}{^\circ}\overrightarrow{m} \right|}{\left| \overrightarrow{n} \right| \cdot \left| \overrightarrow{m} \right|}$,
wobei n und m die Normalenvektoren der Ebenen sind.

Kreise und Kugeln in der analytischen Geometrie

Gleichungen

Kreis

$$\left( \overrightarrow{x} - \overrightarrow{m} \right)^{2} = r^{2}$$

Alle Punkte im zweidimensionalen Raum, deren Vektoren zum Mittelpunkt die Länge des Radius haben, liegen auf dem Kreis. Umgeschrieben ergibt sich:

$$\left( x_{1} - m_{1} \right)^{2} + \left( x_{2} - m_{2} \right)^{2} = r^{2}$$

Kugel

Im dreidimensionalen Raum legt die Form $\left( \overrightarrow{x} - \overrightarrow{m} \right)^{2} = r^{2}$ nach dem gleichen Prinzip wie bei dem Kreis eine Kugel fest. Es ergibt sich:

$$\left( x_{1} - m_{1} \right)^{2} + \left( x_{2} - m_{2} \right)^{2} + \left( x_{3} - m_{3} \right)^{2} = r^{2}$$

Für die Lage eines in die Gleichung eingesetzten Punktes zur Kugel ergeben sich drei Möglichkeiten:

1. Auf der Kugel -> die Gleichung ist erfüllt

2. In der Kugel -> das Ergebnis ist zu klein

3. Außerhalb der Kugel -> das Ergebnis ist zu groß

Falls die Gleichung für die Kugel nicht in der hier aufgeführten Form vorliegt, so kann durch quadratische Ergänzung zu dieser gelangt werden.

Lagebeziehungen

Für die Lagebeziehungen werden meist die Abstände und Radien der Objekte betrachtet.

Kugel zur Ebene

Hier gibt es drei Fälle:

1. Schnittkreis

2. Tangentialebene (Berührung in einem Punkt)

3. Kein Schnittpunkt

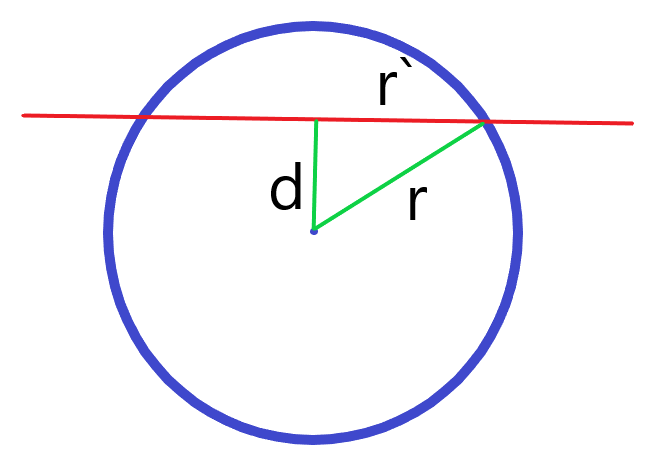
Hierzu wird der kürzeste Abstand d vom Mittelpunkt der Kugel zu der Ebene berechnet und mit dem Radius verglichen. Für die Fälle gilt:

1. Der Punkt auf der Ebene mit dem kürzesten Abstand zum Mittelpunkt des Kreises ist der Mittelpunkt des Schnittkreises. Zum Bestimmen kann der Normalenvektor der Ebene als Einheitsvektor mit dem Abstand (herausgefunden durch die Hessesche Normalenform der Ebene) multipliziert auf den Mittelpunkt addiert werden. Der Radius des Schnittkreises wird über den Satz des Pythagoras bestimmt.

Quelle: unsicher (evtl. aus dem Internet, allerdings nicht erneut über die Bildersuche etc. gefunden)

Aus der Skizze ergibt sich: $r^{2} = d^{2} + {r´}^{2}$. Hieraus folgt für den Radius des Schnittkreises: $r´ = \sqrt{\ r^{2} - d^{2}}$

2. $r = d$

3. $r < d$

Kugel zu Gerade

Die Parametergleichung der Geraden wird in die Kugelgleichung eingesetzt.

Keine Lösung → kein gemeinsamer Punkt

Eine Lösung → Gerade berührt Kugel

Zwei Lösungen → Gerade schneidet Kugel

Bilden einer Tangentialebene

Ist ein Punkt auf der Kugel gegeben, so lässt sich mit Hilfe dieses eine Tangentialebene zur Kugel bilden. Der Vektor vom Mittelpunkt der Kugel zum gegebenen Punkt stellt hierbei den Normalenvektor und der gegebene Punkt den Stützvektor dar.

Polarebene

Die Berührpunkte aller Tangenten von einem Punkt außerhalb der Kugel an die Kugel bilden einen Kreis beziehungsweise eine Polarebene. Es gilt:

$$E:\left( \overrightarrow{x} - \overrightarrow{m} \right) \cdot \left( \overrightarrow{p} - \overrightarrow{m} \right) = r^{2}$$

$$\overrightarrow{p} = Vektor\ des\ Punktes\ außerhalb\ der\ Kugel$$

$$\overrightarrow{m} = Mittelpunkt\ der\ Kugel$$

$$r = Radius\ der\ Kugel$$