Mathe → Analytische Geometrie →
Geraden - Formen und Punktprobe
Parameterform
Über diese Gleichung sind alle Punkte auf der Geraden definiert, sie sind vom Ortsvektor aus über den Richtungsvektor zu erreichen.
Normalenform
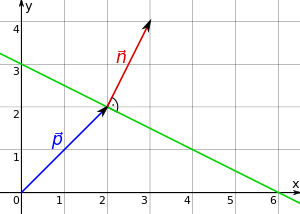
Eine Gerade im zweidimensionalen Raum kann durch die Normalenform bestimmt werden. Sie kann durch einen Stützvektor , welcher der Ortsvektor eines auf der Gerade liegenden Punktes ist und den Normalenvektor , welcher mit der Gerade einen rechten Winkel bildet, dargestellt werden.
Ein Punkt für dessen Ortsvektor gilt, liegt auf der Gerade.
Berechnung aus der Parameterform
Der Stützvektor bleibt gleich. Für den Normalenvektor werden die Komponenten des Richtungsvektors und bei einer Komponente das Vorzeichen vertauscht.
Koordinatenform
Im zweidimensionalen Raum kann eine Gerade auch durch die Koordinatenform beziehungsweise als lineare Gleichung durch drei reelle Zahlen beschrieben werden.
Diese Form entsteht durch ausmultiplizieren der Normalenform.
Punktprobe
Punkt mit Geradengleichung gleichsetzen, t berechnen (muss für jede ,,Zeile“ gleich sein).
Sie möchten mir einen Kaffee spendieren?
Anmerkungen oder sonstige Ideen und Vorschläge können Sie gern per Mail an info@lernzettel.org bzw. fehler@lernzettel.org senden.