Ableiten

Mit der Ableitung wird eine Funktion erzeugt, welche an allen Stellen die Steigung der ursprünglichen Funktion zeigt. Der weitere Nutzen von Ableitungen wird unter Kurvendiskussion ersichtlich.

Ableitungsregeln

Seien f, g und h differenzierbare, reelle Funktionen, n und a reelle Zahlen, dann gilt:

Konstante Funktionen

$$\left( a \right)´ = 0$$

Potenzregel

$$\left( x^{n} \right)´ = nx^{n - 1}$$

Faktorregel

$$\left( a \cdot f \right)´ = a \cdot f´$$

Summenregel

$$\left( g \pm h \right)´ = g´ \pm h´$$

Kettenregel

$$\left( g \circ h \right)´\left( x \right) = (g\left( h\left( x \right) \right)´ = g´(h\left( x \right)) \cdot h´(x)$$

Produktregel

$$\left( g \cdot h \right)´ = g´ \cdot h + g \cdot h´$$

Quotientenregel

$$\left( \frac{g}{h} \right)´ = \frac{g´ \cdot h - g \cdot h´}{h^{2}}$$

Ableiten der e-Funktion

Die e-Funktion wird nach der Kettenregel abgeleitet, wobei die Ableitung der äußeren Funktion $e^{x}$ wieder $e^{x}$ ist.

Beispiel:  $f\left( x \right) = e^{2x^{2} + 3}$
$f´\left( x \right) = 4x \cdot e^{2x^{2} + 3}$

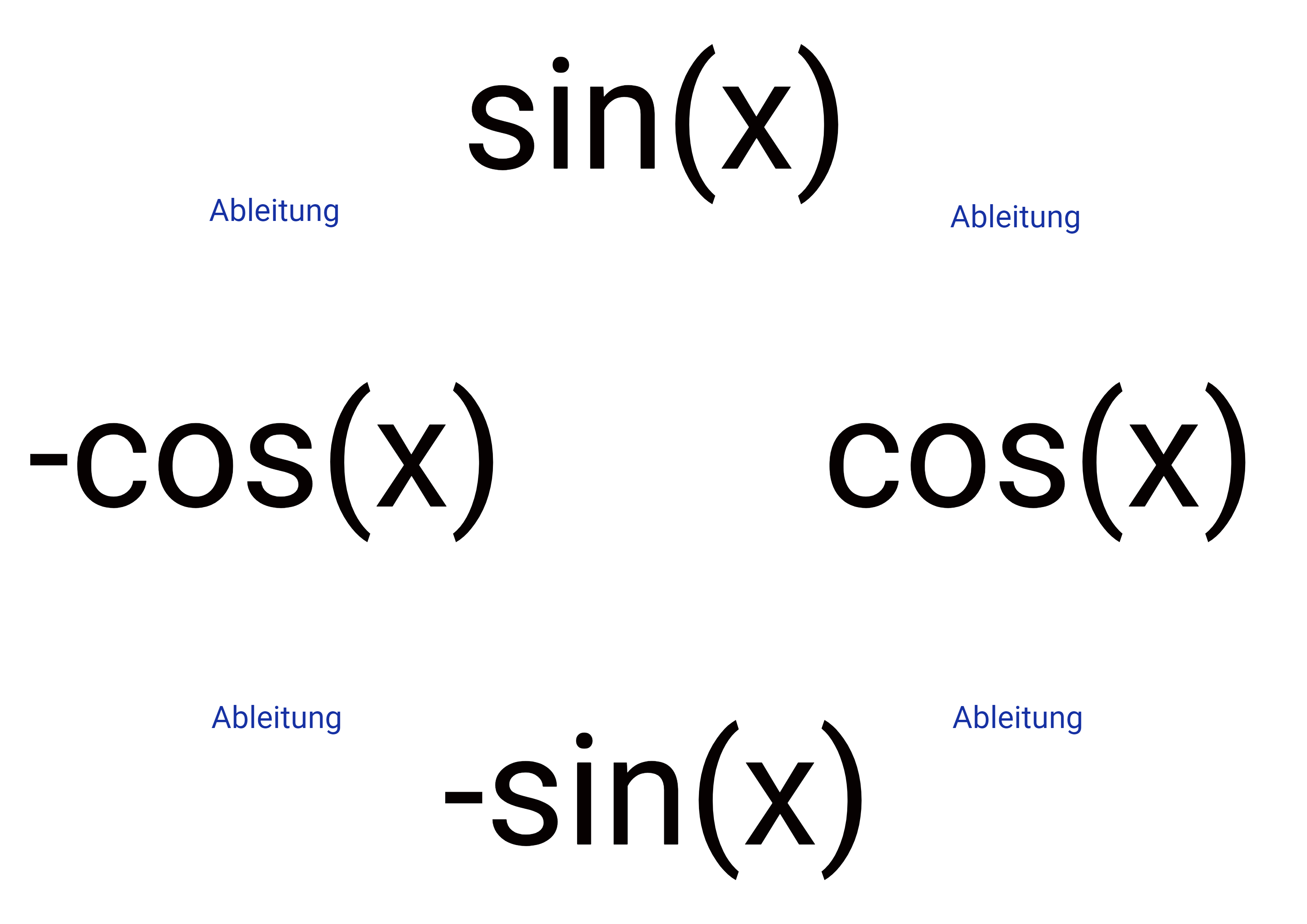
Ableiten der trigonometrischen Funktion

Auch hier wird nach der Kettenregel abgeleitet, wobei für die äußere Funktion gilt (gelesen im Uhrzeigersinn):

Beispiel:  $f\left( x \right) = sin(2x)$ $f´\left( x \right) = 2 \cdot cos(2x)$